
4、一个等差数列的前n项和为48,前2n项和为60,则它的前3n项和为( )
A.-24 B.84 C.72 D.36
3、方程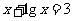 的解
的解 ( )
( )
A.(0,1) B.(1,2) C.(2,3) D.(3,+∞)
1、已知α、β都是第二象限角,且cosα>cosβ,则( )
A.α<β B.sinα>sinβ
C.tanα>tanβ D.cotα<cotβ
2 已知
已知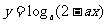 在[0,1]上是
在[0,1]上是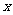 的减函数,则a的取值范围是( )
的减函数,则a的取值范围是( )
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
9.已知5个数成等差数列,它们的和为5,平方和为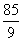 ,求这5个数
,求这5个数
解:设三个数为a,公差为d,则这5个数依次为a-2d,a-d ,a ,a+d
,a+2d 依题意:
依题意:
(a-2d)2
+(a-d)2 + a2 + (a+d)2 + (a+2d)2 =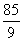
且(a-2d) + (a-d) + a + (a+d) + (a+2d) = 5
即 a2+2d2 = 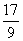 且 a=1
且 a=1
∴a=1且d=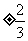
当d=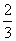 时,这5个数分别是-
时,这5个数分别是-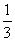 、
、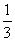 、1、
、1、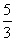 、
、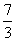 ;
;
当d=-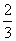 时,这5个数分别是
时,这5个数分别是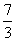 、
、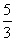 、1、
、1、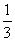 、-
、-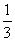

(2006江苏)设数列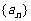 、
、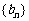 、
、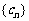 满足:
满足: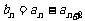 ,
,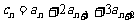 (n=1,2,3,…),证明
(n=1,2,3,…),证明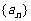 为等差数列的充分必要条件是
为等差数列的充分必要条件是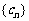 为等差数列且
为等差数列且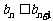 (n=1,2,3,…)
(n=1,2,3,…)
证明:必要性.设{a n}是公差为 d1的等差数列,则
b n+1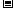 b
n = (a n+1
b
n = (a n+1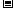 a
n+3)
a
n+3)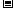 (a
n
(a
n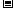 a
n+2)=(a n+1
a
n+2)=(a n+1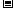 a
n)
a
n)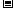 (a
n+3
(a
n+3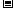 a
n+2)=d1
a
n+2)=d1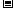 d1=0
d1=0
所以b n≤b n+1 (n=1,2,3,…)成立.
又c n+1-c n=(a n+1-a n)+2(a n+2-a n+1)+3(a n+3-a n+2)
=d1+2d1+3d1=6d1(常数)(n=1,2,3,…),
所以数列{c n}为等差数列.
充分性。设数列{c n}是公差为d2的等差数列,且b n≤b n+1 (n=1,2,3,…).
证法一:
∵c n= a n +2a n+1+3a n+2 ①
∴c n+2= a n+2+2a n+3+3a n+4 ②
①-②得c n - c n+2=( a n - a n+2)+2(a n+1 - a n+3)+3(a n+2 - a n+4)
= b n + 2b n+1 + 3b n+2.
∵c n- c n+2=( c n- c n+1)+( c n+1 - c n+2)=-2d2.
∴bn + 2bn+1 + 3bn+2 =-2d2. ③
从而有
bn+1 + 2bn+2 + 3bn+3 =-2d2. ④
④-③得
(b n+1 - b n)+2(b n+2 - b n+1)+3(b n+3 - b n+2)=0. ⑤
∵b n+1 - b n≥0,b n+2 - b n+1≥0, b n+3 - b n+2≥0,
∴由⑤得b n+1 - b n=0(n=1,2,3,…).
由此不妨设b n =d3(n=1,2,3,…),则a n - a n+2 =d3(常数).
由此c n = a n + 2a n+1 + 3a n+2 = 4a n + 2a n+1 – 3d3,
从而c n+1 = 4a n+1 + 2a n+2 - 3d3 = 4a n+1 + 2a n -5d3.
两式相减得c n+1 - c n =2(a n+1 - a n)-2d3,
因此a n+1 - a n =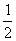 (c n+1-cn)+d3=
(c n+1-cn)+d3=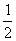 d2+d3(常数)(n=1,2,3,…),
d2+d3(常数)(n=1,2,3,…),
所以数列{a n}是等差数列.
证法二:
令An = a n+1- a n,由b n≤b n+1知a n - a n+2≤a n+1- a n+3,
从而a n+1- a n≥a n+3 - a n+2,即An≥An+2(n=1,2,3,…).
由c n = a n + 2a n+1 + 3a n+2, c n+1 = a n+1 + 2a n+2 + 3a n+3得
c n+1-c n=( a n+1- a n)+2(a n+2- a n+1)+3(a n+3 - a n+2),即
An+2An+1+3An+2=d2. ⑥
由此得
An+2+2An+3+3An+4=d2. ⑦
⑥-⑦得
(An-An+2)+2(An+1- An+3)+3(An+2- An+4)=0. ⑧
因为An-An+2≥0,An+1- An+3≥0,An+2- An+4≥0,
所以由⑧得An-An+2=0(n=1,2,3,…).
于是由⑥得
4An+2An+1=An+2An+1+3An+2=d2, ⑨
从而
2An+4An+1=4An+1+2An+2=d2. ⑩
由⑨和⑩得4An+2An+1=2An+4An+1,故An+1= An ,即
a n+2- a n+1= a n+1- a n(n=1,2,3,…),
所以数列{a n}是等差数列.
8.设等差数列{an}的前n项和为Sn 已知a3=12, S12>0,S13<0
(Ⅰ)求公差d的取值范围;
(Ⅱ)指出S1,S2,…,S12,中哪一个值最大,并说明理由
解: (Ⅰ)依题意,有
已知a3=12, S12>0,S13<0
(Ⅰ)求公差d的取值范围;
(Ⅱ)指出S1,S2,…,S12,中哪一个值最大,并说明理由
解: (Ⅰ)依题意,有 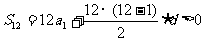
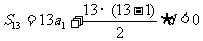 ,即
,即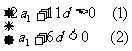 由a3=12,得 a1=12-2d
(3)将(3)式分别代入(1),(2)式,得
由a3=12,得 a1=12-2d
(3)将(3)式分别代入(1),(2)式,得  ,∴
,∴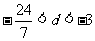
 (Ⅱ)由d<0可知 a1>a2>a3>…>a12>a13
(Ⅱ)由d<0可知 a1>a2>a3>…>a12>a13 因此,若在1≤n≤12中存在自然数n,使得an>0,an+1<0,
则Sn就是S1,S2,…,S12中的最大值
因此,若在1≤n≤12中存在自然数n,使得an>0,an+1<0,
则Sn就是S1,S2,…,S12中的最大值 由于 S12=6(a6+a7)>0, S13=13a7<0,即
a6+a7>0, a7<0
由于 S12=6(a6+a7)>0, S13=13a7<0,即
a6+a7>0, a7<0 由此得 a6>-a7>0
由此得 a6>-a7>0 因为a6>0, a7<0,故在S1,S2,…,S12中S6的值最大
因为a6>0, a7<0,故在S1,S2,…,S12中S6的值最大
7.(2003年春季上海,12)设f(x)= ,利用课本中推导等差数列前n项和的公式的方法,可求得f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值为________.
,利用课本中推导等差数列前n项和的公式的方法,可求得f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值为________.
解析:倒序相加法,观察函数解析式的特点,得到f(x)+f(1-x)=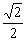 ,即f(-5)+
f(6)=
,即f(-5)+
f(6)=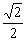 ,f(-4)+f(5)=
,f(-4)+f(5)=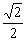 ,f(-3)+f(4)=
,f(-3)+f(4)=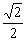 ,f(-2)+f(3)=
,f(-2)+f(3)=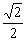 ,f(-1)+
f(2)=
,f(-1)+
f(2)=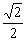 ,f(0)+f(1)=
,f(0)+f(1)=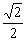 ,故所求的值为3
,故所求的值为3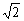 .
.
答案:3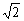
3.(2004年春季上海,7)在数列{an}中,a1=3,且对任意大于1的正整数n,点(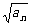 ,
,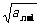 )在直线x-y-
)在直线x-y-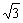 =0上,则an=___________________.
=0上,则an=___________________.
解析:将点代入直线方程得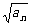 -
-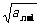 =
=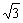 ,由定义知{
,由定义知{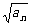 }是以
}是以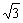 为首项,以
为首项,以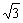 为公差的等差数列,故
为公差的等差数列,故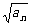 =
=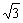 n,即an=3n2.
n,即an=3n2.
答案:3n2
6.在等差数列{an}中,公差为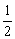 ,且a1+a3+a5+…+a99=60,则a2+a4+a6+…+a100=_________.
,且a1+a3+a5+…+a99=60,则a2+a4+a6+…+a100=_________.
解析:由等差数列的定义知a2+a4+a6+…+a100=a1+a3+a5+…+a99+50d=60+25=85.
答案:85
10.数列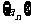 的首项
的首项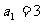 ,通项
,通项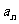 与前n项和
与前n项和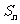 之间满足
之间满足
(1)求证: 是等差数列,并求公差;
是等差数列,并求公差;
(2)求数列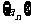 的通项公式;
的通项公式;
(3)数列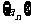 中是否存在正整数k,使得不等式
中是否存在正整数k,使得不等式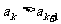 对任意不小于k的正整数都成立?若存在,求出最小的k,若不存在,请说明理由.
对任意不小于k的正整数都成立?若存在,求出最小的k,若不存在,请说明理由.
解:(1)当
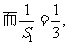
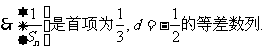
(2)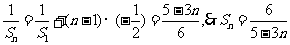
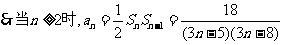

(3)
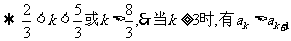 所求最小k=3.
所求最小k=3.
[探索题]已知数列{an}的各项均为正整数,且满足an+1=an2-2nan+2(n∈N*),又a5=11.
(1)求a1,a2,a3,a4的值,并由此推测出{an}的通项公式(不要求证明);
(2)设bn=11-an,Sn=b1+b2+…+bn,Sn′=|b1|+|b2|+…+|bn|,求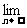
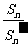 的值.
的值.
解:(1)由a5=11,得11=a42-8a4+2,即a42-8a4-9=0.解得a4=9或a4=-1(舍).
由a4=9,得a32-6a3-7=0.
解得a3=7或a3=-1(舍).
同理可求出a2=5,a1=3.
由此推测an的一个通项公式an=2n+1(n∈N*).
(2)bn=11-an=10-2n(n∈N*),可知数列{bn}是等差数列.
Sn=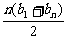 =
=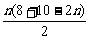 =-n2+9n.
=-n2+9n.
当n≤5时,Sn′=Sn=-n2+9n;
当n>5时,Sn′=-Sn+2S5=-Sn+40=n2-9n+40.
当n≤5时,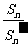 =1;
=1;
备选题
9.已知数列{an}的前n项和Sn=n2-2n,bn= ,
,
证明:数列{bn}是等差数列.
证明:Sn=n2-2n,a1=S1=-1.
当n≥2时,an=Sn-Sn-1=n2-2n-(n-1)2+2(n-1)=2n-3,a1满足上式即an=2n-3.
∵an+1-an=2(n+1)-3-2n+3=2,
∴数列{an}是首项为-1,公差为2的等差数列.
∴a2+a4+…+a2n=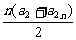
=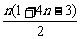 =n(2n-1),
=n(2n-1),
即bn=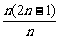 =2n-1.
=2n-1.
∴bn+1-bn=2(n+1)-1-2n+1=2.
又b2=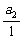 =1,
=1,
∴{bn}是以1为首项,2为公差的等差数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com