
3.运算律
⑴ 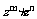 =
.
=
.
⑵ 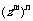 =
.
=
.
⑶ 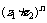 =
=
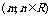 .
.
|
例1.计算: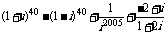
解:提示:利用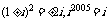
原式=0
变式训练1:求复数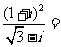
(A)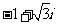 (B)
(B)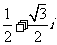 (C)
(C)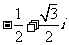 (D)
(D)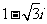
解: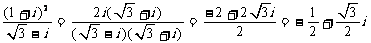 故选C;
故选C;
例2. 若 ,求
,求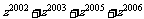
解:提示:利用
原式=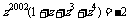
变式训练2:已知复数z满足z2+1=0,则(z6+i)(z6-i)= ▲ .
解:2
例3. 已知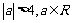 ,问是否存在复数z,使其满足
,问是否存在复数z,使其满足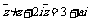 (a
(a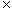 R),如果存在,求出z的值,如果不存在,说明理由
R),如果存在,求出z的值,如果不存在,说明理由
解:提示:设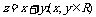 利用复数相等的概念有
利用复数相等的概念有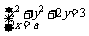
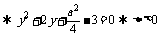
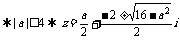
变式训练3:若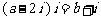 ,其中
,其中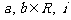 是虚数单位,则a+b=__________
是虚数单位,则a+b=__________
解:3
例4. 证明:在复数范围内,方程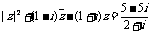 (
(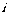 为虚数单位)无解.
为虚数单位)无解.
证明:原方程化简为
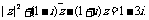 设
设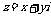
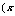 、y∈R,代入上述方程得
、y∈R,代入上述方程得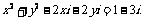
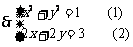 将(2)代入(1),整理得
将(2)代入(1),整理得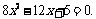
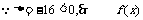 无实数解,∴原方程在复数范围内无解.
无实数解,∴原方程在复数范围内无解.
变式训练4:已知复数z1满足(1+i)z1=-1+5i,z2=a-2-i,其中i为虚数单位,a∈R, 若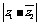 <
<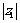 ,求a的取值范围.
,求a的取值范围.
解:由题意得 z1=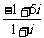 =2+3i,
=2+3i,
于是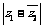 =
=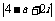 =
=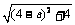 ,
,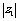 =
=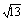 .
.
|
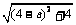 <
<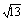 ,得a2-8a+7<0,1<a<7.
,得a2-8a+7<0,1<a<7.2.几个重要的结论:
⑴ 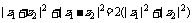
⑵ 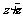 =
=
.
=
=
.
⑶ 若z为虚数,则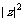 =
= 
1.复数的加、减、乘、除运算按以下法则进行:
设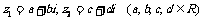 ,则
,则
(1) 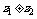 =
;
=
;
(2) 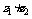 =
;
=
;
(3) 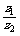 =
(
=
(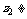 ).
).
2.设z=a+bi (a,b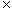 R),利用复数相等和有关性质将复数问题实数化是解决复数问题的常用方法.
R),利用复数相等和有关性质将复数问题实数化是解决复数问题的常用方法.
第2课时 复数的代数形式及其运算
|
1.要理解和掌握复数为实数、虚数、纯虚数、零时,对实部和虚部的约束条件.
8.两个实数可以比较大小、但两个复数如果不全是实数,就 比较它们的大小.
|
例1. m取何实数值时,复数z=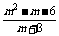 +
+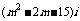 是实数?是纯虚数?
是实数?是纯虚数?
解:① z是实数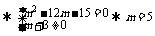
② z为纯虚数

变式训练1:当m分别为何实数时,复数z=m2-1+(m2+3m+2)i是(1)实数?(2)虚数?(3)纯虚数?(4)零?
解:(1)m=-1,m=-2;(2)m≠-1,m≠-2;(3)m=1;(4)m=-1.
例2. 已知x、y为共轭复数,且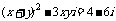 ,求x.
,求x.
解:设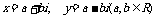 代入由复数相等的概念可得
代入由复数相等的概念可得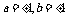
变式训练2:已知复数z=1+i,如果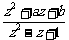 =1-i,求实数a,b的值.
=1-i,求实数a,b的值.
由z=1+i得
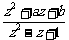 =
=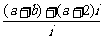 =(a+2)-(a+b)i
=(a+2)-(a+b)i
从而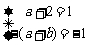 ,解得
,解得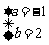 .
.
例3. 若方程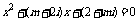 至少有一个实根,试求实数m的值.
至少有一个实根,试求实数m的值.
解:设实根为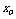 ,代入利用复数相等的概念可得
,代入利用复数相等的概念可得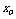 =
=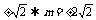
变式训练3:若关于x 的方程x2+(t2+3t+tx )i=0有纯虚数根,求实数t的值和该方程的根.
解:t=-3,x1=0,x2=3i.提示:提示:设出方程的纯虚数根,分别令实部、虚部为0,将问题转化成解方程组.
例4. 复数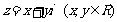 满足
满足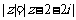 ,试求
,试求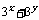 的最小值.
的最小值.
设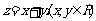 ,则
,则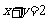 ,
,
于是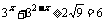
变式训练4:已知复平面内的点A、B对应的复数分别是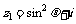 、
、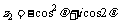 ,其中
,其中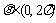 ,设
,设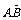 对应的复数为
对应的复数为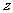 .
.
(1) 求复数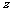 ;
;
(2) 若复数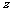 对应的点P在直线
对应的点P在直线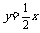 上,求
上,求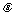 的值.
的值.
解:(1) 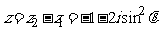
(2) 将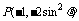 代入
代入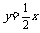
可得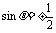
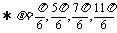 .
.
|
7.复数z=a+bi(a, b R)与复平面上的点 建立了一一对应的关系.
R)与复平面上的点 建立了一一对应的关系.
6.复平面:建立直角坐标系来表示复数的平面叫做复平面, x轴叫做 , 叫虚轴.
5.若z=a+bi, (a, b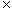 R), 则 | z |=
; z
R), 则 | z |=
; z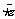 =
.
=
.
4.共轭复数:当两个复数实部 ,虚部 时.这两个复数互为共轭复数.(当虚部不为零时,也可说成互为共轭虚数).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com