3．实数与向量的积

⑴ 实数与向量的积是一个向量，记作．它的长度与方向规定如下：

① | 　|＝　　　　　 ．

② 当＞0时，的方向与的方向　　　　 ；

　 当＜0时，的方向与的方向　　　　 ；

　 当＝0时，　　　　 ．

⑵ (μ)＝　　　　　 ．

　 (+μ)＝　　　　　 ．

　 (+)＝　　　　　 ．

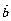⑶ 共线定理：向量与非零向量共线的充要条件是有且只有一个实数λ使得　　　　 ．

2．向量的加法与减法

⑴ 求两个向量的和的运算，叫向量的加法．向量加法按　　　　 法则或　　　　　　　　　 法则进行．加法满足　　　　　　 律和　　　　 律．

⑵ 求两个向量差的运算，叫向量的减法．作法是将两向量的　　　　　 重合，连结两向量的　　　　 ，方向指向　　　　　　　　 ．

1．向量的有关概念

⑴ 既有　　　 又有　　　 的量叫向量．　　　　

　　　　　 的向量叫零向量．　　　　　　　　 的向量，叫单位向量．

⑵ 　　　　　　　　　叫平行向量，也叫共线向量．规定零向量与任一向量　　　　 ．

⑶ 　　　　　　且　　　　　 的向量叫相等向量．

4．正弦定理、余弦定理及利用三角公式进行恒等变形的能力．以化简、求值或判断三角形的形状为主．解三角形常常作为解题工具用于立体几何中的计算或证明．

第1课时　　 向量的概念与几何运算

3．向量和其它数学知识的结合．如和三角函数、数列、曲线方程等及向量在物理中的应用．

2．向量的坐标运算及应用．

1．平面向量的性质和运算法则，共线定理、基本定理、平行四边形法则及三角形法则．

7．掌握正、余弦定理，并能初步运用它们解斜三角形．

向量由于具有几何形式与代数形式的“双重身份”，使它成为中学数学知识的一个交汇点，成为多项内容的媒介．

主要考查：

6．掌握平面两点间的距离公式以及线段的定比分点和中点坐标公式，并且能熟练运用；掌握平移公式．

5．掌握平面向量的数量积及其几何意义，了解用平面向量的数量积可以处理有关长度、角度和垂直的问题，掌握向量垂直的条件．