
3.利用等可能性的概率公式,关键在于寻找基本事件数和有利事件数.
|
2.如果一次试验中共有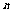 种等可能出现的结果,其中事件A包含的结果有m种,那么事件A的概率
种等可能出现的结果,其中事件A包含的结果有m种,那么事件A的概率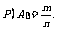 从集合的角度看,一次试验中等可能出现的所有结果组成一个集合I,其中事件A包含的结果组成I的一个子集A,因此
从集合的角度看,一次试验中等可能出现的所有结果组成一个集合I,其中事件A包含的结果组成I的一个子集A,因此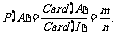 从排列、组合的角度看,m、n实际上是某些事件的排列数或组合数.因此这种“古典概率”的问题,几乎使有关排列组合的计算与概率的计算成为一回事.
从排列、组合的角度看,m、n实际上是某些事件的排列数或组合数.因此这种“古典概率”的问题,几乎使有关排列组合的计算与概率的计算成为一回事.
1.实际生活中所遇到的事件包括必然事件、不可能事件及随机事件.随机事件在现实世界中是广泛存在的.在一次试验中,事件是否发生虽然带有偶然性,当在大量重复试验下,它的发生呈现出一定的规律性,即事件发生的频率总是接近于某个常数,这个常数就叫做这个事件的概率.
2.等可能性事件的概率
(1) 基本事件:一次试验连同其中可能出现的每一个结果称为一个基本事件.
(2) 等可能性事件的概率:如果一次试验由n个基本事件组成,而且所有结果出现的可能性都相等,那么每一个基本事件的概率是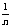 .如果某个事件A包含的结果有m个,那么事件A的概率:
.如果某个事件A包含的结果有m个,那么事件A的概率: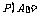
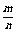
|
例1.1) 一个盒子装有5个白球3个黑球,这些球除颜色外,完全相同,从中任意取出两个球,求取出的两个球都是白球的概率;
(2) 箱中有某种产品a个正品,b个次品,现有放回地从箱中随机地连续抽取3次,每次1次,求取出的全是正品的概率是( )
A.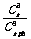 B.
B.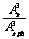 C.
C.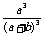 D.
D.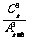
(3) 某班有50名学生,其中15人选修A课程,另外35人选修B课程,从班级中任选两名学生,他们是选修不同课程的学生的概率是多少?
解:(1)从袋内8个球中任取两个球共有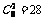 种不同结果,从5个白球中取出2个白球有
种不同结果,从5个白球中取出2个白球有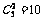 种不同结果,则取出的两球都是白球的概率为
种不同结果,则取出的两球都是白球的概率为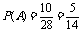
(2)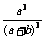 (3)
(3)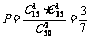
变式训练1. 盒中有1个黑球9个白球,它们除颜色不同外,其它没什么差别,现由10人依次摸出1个球,高第1人摸出的是黑球的概率为P1,第10人摸出是黑球的概率为P10,则 ( )
A.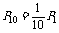 B.
B.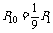
C.P10=0 D.P10=P1
解:D
例2. 甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球,两甲、乙两袋中各任取2个球.
(1) 若n=3,求取到的4个球全是红球的概率;
(2) 若取到4个球中至少有2个红球的概率为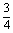 ,求n.
,求n.
解:(1)记“取到的4个球全是红球”为事件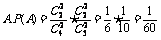 .
.
(2)记“取到的4个球至多有1个红球”为事件B,“取到的4个球只有1个红球”为事件B1,“取到的4个球全是白球”为事件B2,由题意,得
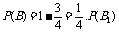
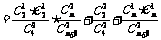
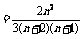
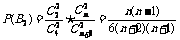
所以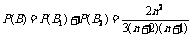
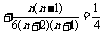 ,化简,得7n2-11n-6=0,解得n=2,或
,化简,得7n2-11n-6=0,解得n=2,或 (舍去),故n=2.
(舍去),故n=2.
变式训练2:在一个口袋中装有5个白球和3个黑球,这些球除颜色外完全相同.从中摸出3个球,至少摸到2个黑球的概率等于 ( )
A.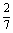 B.
B.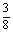
C.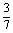 D.
D.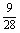
解:A
例3. 袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球取出的可能性都相等,用 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求:
(1) 取出3个小球上的数字互不相同的概率;
(2) 计分介于20分到40分之间的概率.
解:(1)“一次取出的3个小球上的数字互不相同”的事件记为A,
则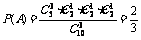
(2)“一次取球所得计分介于20分到40分之间”的事件记为C,则P(C)=P(“ =3”或“
=3”或“ =4”)=P(“
=4”)=P(“ =3”)+P(“
=3”)+P(“ =4”)=
=4”)=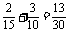
变式训练3:从数字1,2,3,4,5中任取3个,组成没有重复数字的三位数,计算:
① 这个三位数字是5的倍数的概率;
②这个三位数是奇数的概率;
③这个三位数大于400的概率.
解:⑴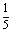 ⑵
⑵ ⑶
⑶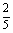
例4. 在一次口试中,要从20道题中随机抽出6道题进行回答,答对了其中的5道就获得优秀,答对其中的4道就可获得及格.某考生会回答20道题中的8道题,试求:
(1)他获得优秀的概率是多少?
(2)他获得及格与及格以上的概率有多大?
解:从20道题中随机抽出6道题的结果数,即是从20个元素中任取6个元素的组合数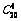 .由于是随机抽取,故这些结果出现的可能性都相等.
.由于是随机抽取,故这些结果出现的可能性都相等.
(1)记“他答对5道题”为事件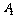 ,由分析过程已知在这
,由分析过程已知在这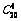 种结果中,他答对5题的结果有
种结果中,他答对5题的结果有 种,故事件
种,故事件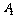 的概率为
的概率为
(2)记“他至少答对4道题”为事件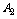 ,由分析知他答对4道题的可能结果为
,由分析知他答对4道题的可能结果为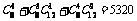 种,故事件
种,故事件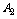 的概率为:
的概率为: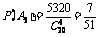
答:他获得优秀的概率为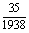 ,获得及格以上的概率为
,获得及格以上的概率为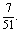
变式训练4:有5个指定的席位,坐在这5个席位上的人都不知道指定的号码,当这5个人随机地在这5个席位上就坐时.
(1) 求5个人中恰有3人坐在指定的席位上的概率;
(2) 若在这5个人侍在指定位置上的概率不小于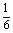 ,则至多有几个人坐在自己指定的席位上?
,则至多有几个人坐在自己指定的席位上?
解:(1)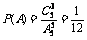
(2)由于3人坐在指定位置的概率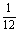 <
<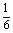 ,故可考虑2人坐在指定位置上的概率,设5人中有2人坐在指定位置上为事件B,则
,故可考虑2人坐在指定位置上的概率,设5人中有2人坐在指定位置上为事件B,则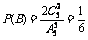 ,又由于坐在指定位置上的人越多其概率越少,而要求概率不小于
,又由于坐在指定位置上的人越多其概率越少,而要求概率不小于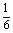 ,则要求坐在指定位置上的人越少越好,故符合题中条件时,至多2人坐在指定席位上.
,则要求坐在指定位置上的人越少越好,故符合题中条件时,至多2人坐在指定席位上.
|
①1.了解随机数的意义,能运用模拟方法估计概率.
②2.了解几何概型的意义.

|
||
|
概率则是概率论入门,目前的概率知识只是为进一步学习概率和统计打好基础,做好铺垫.学习中要注意基本概念的理解,要注意与其他数学知识的联系,要通过一些典型问题的分析,总结运用知识解决问题的思维规律.纵观近几年高考,概率的内容在选择、填空解答题中都很有可能出现。
第1课时 随机事件的概率
|
1.随机事件及其概率
(1) 必然事件:在一定的条件下必然发生的事件叫做必然事件.
(2) 不可能事件:在一定的条件下不可能发生的事件叫做不可能事件.
(3) 随机事件:在一定的条件下,也可能发生也可能不发生的事件叫做随机事件.
(4) 随机事件的概率:一般地,在大量重复进行同一试验时,事件A发生的频率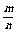 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件,这时就把这个常数叫做事件
总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件,这时就把这个常数叫做事件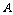 的概率,记作
的概率,记作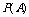 .
.
(5) 概率从数量上反映了一个事件发生的可能性的大小,它的取值范围是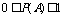 ,必然事件的概率是1,不可能事件的概率是0.
,必然事件的概率是1,不可能事件的概率是0.
①1.理解古典概型及其概率计算公式.
②2.会计算一些随机事件所含的基本事件数及事件发生的概率。
2.了解互斥事件、对立事件的意义及其运算公式.
1.了解随机事件发生的不确定性和频率的稳定性,了解概率的意义,了解频率与概率的区别。
2. 间接证明:间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法;反证法即从 开始,经过正确的推理,说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法(归谬法).
|
例1.若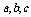 均为实数,且
均为实数,且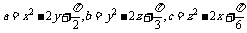 。
。
求证: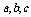 中至少有一个大于0。
中至少有一个大于0。
答案:(用反证法)
假设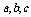 都不大于0,即
都不大于0,即 ,则有
,则有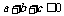 ,
,
而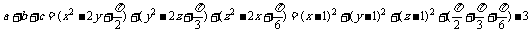 =
=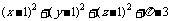
∴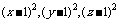 均大于或等于0,
均大于或等于0,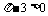 ,∴
,∴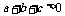 ,这与假设
,这与假设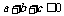 矛盾,故
矛盾,故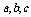 中至少有一个大于0。
中至少有一个大于0。
变式训练1:用反证法证明命题“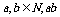 可以被5整除,那么
可以被5整除,那么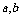 中至少有一个能被5整除。”那么假设的内容是
中至少有一个能被5整除。”那么假设的内容是
答案:a,b中没有一个能被5整除。解析:“至少有n个”的否定是“最多有n-1个”。
例2. △ABC的三个内角A、B、C成等差数列,
求证: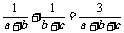 。
。
答案:证明:要证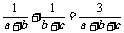 ,即需证
,即需证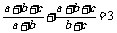 。
。
即证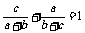 。
。
又需证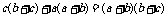 ,需证
,需证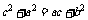
∵△ABC三个内角A、B、C成等差数列。∴B=60°。
由余弦定理,有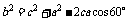 ,即
,即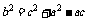 。
。
∴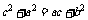 成立,命题得证。
成立,命题得证。
变式训练2:用分析法证明:若a>0,则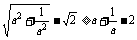 。
。
答案:证明:要证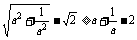 ,
,
只需证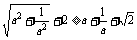 。
。
∵a>0,∴两边均大于零,因此只需证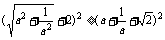
只需证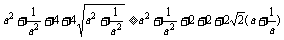 ,
,
只需证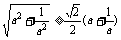 ,只需证
,只需证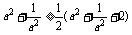 ,
,
即证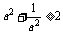 ,它显然成立。∴原不等式成立。
,它显然成立。∴原不等式成立。
例3.已知数列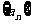 ,
,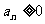 ,
,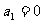 ,
,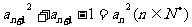 .
.
记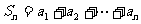 .
.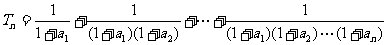 .
.
求证:当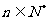 时,
时,
(1)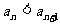 ;
;
(2)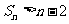 ;
;
(3)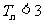 。
。
解:(1)证明:用数学归纳法证明.
①当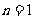 时,因为
时,因为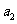 是方程
是方程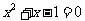 的正根,所以
的正根,所以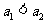 .
.
②假设当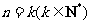 时,
时,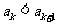 ,
,
因为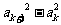
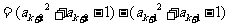
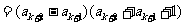 ,
,
所以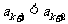 .
.
即当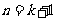 时,
时,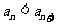 也成立.
也成立.
根据①和②,可知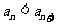 对任何
对任何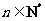 都成立.
都成立.
(2)证明:由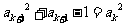 ,
,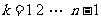 (
( ),
),
得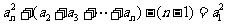 .
.
因为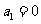 ,所以
,所以 .
.
由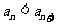 及
及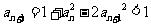 得
得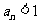 ,
,
所以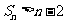 .
.
(3)证明:由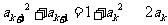 ,得
,得
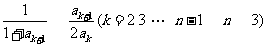
所以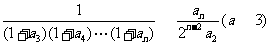 ,
,
于是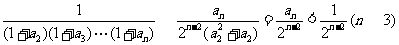 ,
,
故当 时,
时,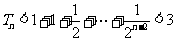 ,
,
又因为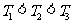 ,
,
所以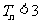 .
.
1.直接证明:直接从原命题的条件逐步推得结论成立,这种证明方法叫直接证明;
直接证明的两种基本方法--分析法和综合法
⑴ 综合法 -- ;⑵分析法 -- ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com