
1.事件A(或B)是否发生对事件B(或A)发生的概率 ,这样的两个事件叫独立事件.
3.在求某些稍复杂的事件的概率时,通常有两种方法:一是将所求事件的概率化成一些彼此互斥事件的概率的和;二是先去求此事件的对立事件的概率.
第3课时 相互独立事件同时发生的概率
|
2.要搞清两个重要公式:
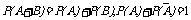 的运用前提.
的运用前提.
1.互斥事件概率的加法公式、对立事件概率的加法公式,都必须在各个事件彼此互斥的前提下使用.
6.由于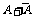 是一个必然事件,再加上
是一个必然事件,再加上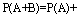
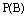 ,故
,故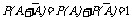 ,于是
,于是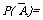 ,这个公式很有用,常可使概率的计算得到简化.当直接求某一事件的概率较为复杂时,可转化去求其对立事件的概率.
,这个公式很有用,常可使概率的计算得到简化.当直接求某一事件的概率较为复杂时,可转化去求其对立事件的概率.
|
例1. 某射手在一次射击训练中,射中10环,9环,8环,7环的概率分别为0.21, 0.23, 0.25, 0.28,计算这个射手在一次射击中:①射中10环或7环的概率;②不够7环的概率.
解:① 0.49;② 0.03.
变式训练1. 一个口袋内有9张大小相同的票,其号数分别是1,2,3, ,9,从中任取2张,其号数至少有1个为偶数的概率等于 ( )
,9,从中任取2张,其号数至少有1个为偶数的概率等于 ( )
A.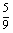 B.
B.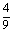
C.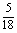 D.
D.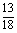
解:D
例2. 袋中有红、黄、白3种颜色的球各1只,从中每次任取1只,有放回地抽取3次,求:
(1)3只全是红球的概率.
(2)3只颜色全相同的概率.
(3)3只颜色不全相同的概率.
(4)3只颜色全不相同的概率.
解:(1)记“3只全是红球”为事件A.从袋中有放回地抽取3次,每次取1只,共会出现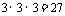 种等可能的结果,其中3只全是红球的结果只有一种,故事件A的概率为
种等可能的结果,其中3只全是红球的结果只有一种,故事件A的概率为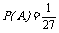 .
.
(2) “3只颜色全相同”只可能是这样三种情况:“3只全是红球”(事件A);“3只全是黄球”(设为事件B);“3只全是白球”(设为事件C).故“3只颜色全相同”这个事件为A+B+C,由于事件A、B、C不可能同时发生,因此它们是互斥事件.再由于红、黄、白球个数一样,故不难得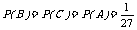 ,
,
故 .
.
(3) 3只颜色不全相同的情况较多,如是两只球同色而另一只球不同色,可以两只同红色或同黄色或同白色等等;或三只球颜色全不相同等.考虑起来比较麻烦,现在记“3只颜色不全相同”为事件D,则事件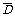 为“3只颜色全相同”,显然事件D与
为“3只颜色全相同”,显然事件D与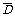 是对立事件.
是对立事件.
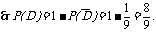
(4) 要使3只颜色全不相同,只可能是红、黄、白各一只,要分三次抽取,故3次抽到红、黄、白各一只的可能结果有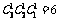 种,故3只颜色全不相同的概率为
种,故3只颜色全不相同的概率为
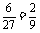 .
.
变式训练2. 从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是 ( )
A.至少有1个黑球与都是黑球
B.至少有1个黑球与至少有1个红球
C.恰有1个黑球与恰有2个黑球
D.至少有1个黑球与都是红球
解:C
例3. 设人的某一特征(如眼睛大小)是由他的一对基因所决定的,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人是纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的一某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:①1个孩子有显性决定特征的概率是多少?②2个孩子至少有一个显性决定特征的概率是多少?
解:①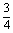 ;②
;②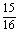
变式训练3. 盒中有6只灯泡,其中2只是次品,4只是正品,从其中任取两只,试求下列事件的概率:
① 取到两只都是次品;
② 取到两只中正品、次品各1只;
③ 取到两只中至少有1只正品.
解:⑴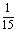 ⑵
⑵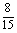 ⑶
⑶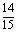
例4. 从男女学生共36名的班级中,任意选出2名委员,任何人都有同样的当选机会,如果选得同性委员的概率等于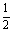 ,求男女相差几名?
,求男女相差几名?
解: 设男生有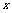 名,则女生有36-
名,则女生有36-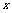 名,选得2名委员都是男生的概率为:
名,选得2名委员都是男生的概率为:
选得2名委员都是女生的概率为
以上两种选法是互斥的,又选得同性委员的概率是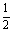
得: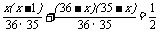
解得: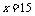 或
或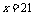
即:男生有15名,女生有21名;或男生有21名,女生有15名.总之,男、女生相差6名.
变式训练4. 学校某班学习小组共10小,有男生若干人,女生若干人,现要选出3人去参加某项调查活动,已知至少有一名女生去的概率为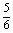 ,求该小组男生的人数?
,求该小组男生的人数?
解:6人
|
5.如果事件A、B互斥,那么事件A+B发生的概率,等于 .即P(A+B)= .
4.由于集合是可以进行运算的,故可用集合表示的事件也能进行某些运算.设A、B是两个事件,那么A+B表示这样一个事件:在同一试验中,A或B中 就表示A+B发生.我们称事件A+B为事件A、B的和.它可以推广如下:“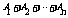 ”表示这样一个事件,在同一试验中,
”表示这样一个事件,在同一试验中,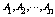 中
即表示
中
即表示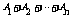 发生,事实上,也只有其中的某一个会发生.
发生,事实上,也只有其中的某一个会发生.
3.从集合的角度看,几个事件彼此互斥,是指由各个事件所含的结果组成的集合彼此
.事件A的对立事件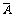 所含的结果组成的集合,是全集中由事件A所含的结果组成的集合的补集.
所含的结果组成的集合,是全集中由事件A所含的结果组成的集合的补集.
2. 的互斥事件叫做对立事件.
1. 的两个事件叫做互斥事件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com