
5.二项分布:如果在一次试验中某事件发生的概率为P,那么在n次独立重复试验中这个事件恰好发生k次的概率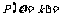 ,有了这个函数,就能写出它的分布列,由于
,有了这个函数,就能写出它的分布列,由于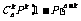 是二项式展开式
是二项式展开式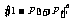 的通项,所以称这个分布为二项分布列,记作
的通项,所以称这个分布为二项分布列,记作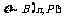
|
例1. 袋子中有1个白球和2个红球.
⑴ 每次取1个球,不放回,直到取到白球为止.求取球次数 的分布列.
的分布列.
⑵ 每次取1个球,放回,直到取到白球为止.求取球次数 的分布列.
的分布列.
⑶ 每次取1个球,放回,直到取到白球为止,但抽取次数不超过5次.求取球次数 的分布列.
的分布列.
⑷ 每次取1个球,放回,共取5次.求取到白球次数 的分布列.
的分布列.
解: ⑴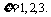
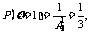
 =
=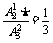
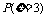 =
=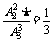
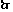 所求
所求 的分布列是
的分布列是
 |
1 |
2 |
3 |
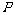 |
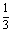 |
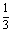 |
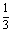 |
⑵ 每次取到白球的概率是
每次取到白球的概率是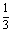 ,不取到白球的概率是
,不取到白球的概率是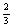 ,
,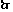 所求的分布列是
所求的分布列是
 |
1 |
2 |
3 |
… |
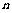 |
… |
|
P |
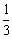 |
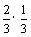 |
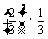 |
… |
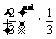 |
… |
⑶
 |
1 |
2 |
3 |
4 |
5 |
|
P |
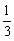 |
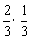 |
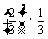 |
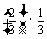 |
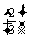 |
⑷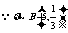
∴ P=( =k)=C5k(
=k)=C5k(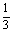 )k·(
)k·(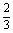 )5-k,
)5-k,
其中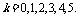
∴所求 的分布列是
的分布列是
 |
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
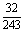 |
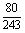 |
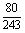 |
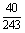 |
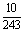 |
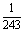 |
变式训练1.  是一个离散型随机变量,其分布列为
是一个离散型随机变量,其分布列为
 |
-1 |
0 |
1 |
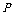 |
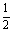 |
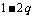 |
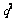 |
则q = ( )
A.1 B.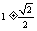
C.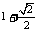 D.
D.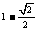
解:D
例2. 一袋中装有6个同样大小的黑球,编号为1,2,3,4,5,6,现从中随机取出3个球,以 表示取出球的最大号码,求
表示取出球的最大号码,求 的分布列.
的分布列.
解:随机变量的取值为3,4,5,6从袋中随机地取3个球,包含的基本事件总数为 ,事件“
,事件“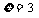 ”包含的基本事件总数为
”包含的基本事件总数为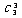 ,事件“
,事件“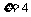 ”包含的基本事件总数为
”包含的基本事件总数为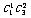 ;事件“
;事件“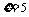 ”包含的基本事件总数为
”包含的基本事件总数为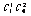 ;事件
;事件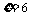 包含的基本事件总数为
包含的基本事件总数为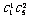 ;从而有
;从而有
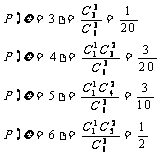
∴随机变量的分布列为:
 |
3 |
4 |
5 |
6 |
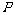 |
 |
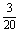 |
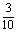  |
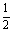 |
变式训练2:现有一大批种子,其中优质良种占30%,从中任取2粒,记 为2粒中优质良种粒数,则
为2粒中优质良种粒数,则 的分布列是
.
的分布列是
.
解:
 |
0 |
1 |
2 |
|
P |
0.49 |
0.42 |
0.09 |
例3. 一接待中心有A、B、C、D四部热线电话,已知某一时刻电话A、B占线的概率均为0.5,电话C、D占线的概率均为0.4,各部电话是否占线相互之间没有影响,假设该时刻有 部电话占线,试求随机变量
部电话占线,试求随机变量 的概率分布.
的概率分布.
解:
 |
0 |
1 |
2 |
3 |
4 |
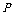 |
0.09 |
0.3 |
0.37 |
0.2 |
0.04 |
变式训练3:将编号为1,2,3,4的贺卡随意地送给编号为一,二,三,四的四个教师,要求每个教师都得到一张贺卡,记编号与贺卡相同的教师的个数为 ,求随机变量
,求随机变量 的概率分布. 解:
的概率分布. 解:
 |
0 |
1 |
2 |
4 |
|
P |
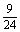 |
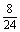 |
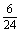 |
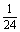 |
|
4.离散型随机变量分布列的性质
(1) 所有变量对应的概率值(函数值)均为非负数,即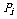 .
.
(2) 所有这些概率值的总和为
即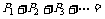 .
.
(3) 根据互斥事件的概率公式,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的
3.从函数的观点来看,P( =xk)=Pk,k=1, 2, …,n,…称为离散型随机变量
=xk)=Pk,k=1, 2, …,n,…称为离散型随机变量 的概率函数或概率分布,这个函数可以用
表示,这个 叫做离散型随机变量的分布列.
的概率函数或概率分布,这个函数可以用
表示,这个 叫做离散型随机变量的分布列.
2.如果随机变量可能取的值 ,那么这样的随机变量叫做离散型随机变量.
1.如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做 ,随机变量通常用希腊字母 ,
,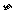 等表示.
等表示.
2.独立重复试验在概率论中占有相当重要地地位,这种试验的结果只有两种,我们主要研究在n次独立重复试验中某事件发生k次的概率: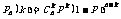 ,其中P是1 次试验中某事件发生的概率,其实
,其中P是1 次试验中某事件发生的概率,其实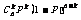 正好是二项式
正好是二项式 的展开式中的第k+1项,很自然地联想起二项式定理.
的展开式中的第k+1项,很自然地联想起二项式定理.
第4课时 离散型随机变量的分布列
|
1.当且仅当事件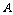 与事件
与事件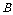 互相独立时,才有
互相独立时,才有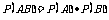 ,故首先要搞清两个事件的独立性.
,故首先要搞清两个事件的独立性.
4.n次独立重复试验中恰好发生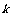 次的概率:如果在一次试验中某事件发生的概率是P,那么在
次的概率:如果在一次试验中某事件发生的概率是P,那么在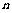 次独立重复试验中这个事件恰好发生
次独立重复试验中这个事件恰好发生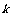 次的概率是
次的概率是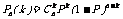 .
.
|
例1. 如图所示,用A、B、C三类不同的元件连接成两个系统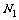 、
、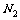 ,当元件A、B、C都正常工作时,系统
,当元件A、B、C都正常工作时,系统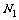 正常工作,当元件A正常工作且元件B、C至少有1个正常工作时系统
正常工作,当元件A正常工作且元件B、C至少有1个正常工作时系统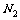 正常工作,已知元件A、B、C正常工作的概率依次为0.8、0.9、0.9,分别求系统
正常工作,已知元件A、B、C正常工作的概率依次为0.8、0.9、0.9,分别求系统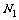 、
、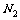 正常工作时的概率.
正常工作时的概率.
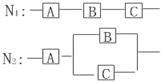
解:分别记元件A、B、C正常工作为事件A、B、C,
由已知条件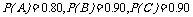
(Ⅰ)因为事件A、B、C是相互独立的,所以,系统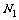 正常工作的概率
正常工作的概率
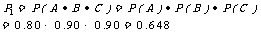 故系统
故系统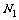 正常工作的概率为0.648.
正常工作的概率为0.648.
(Ⅱ)系统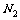 正常工作的概率
正常工作的概率
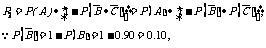
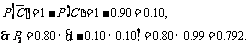
故系统正常工作的概率为0.792.
变式训练1. 有甲、乙两地生产某种产品,甲地的合格率为90%,乙地的合格率为92%,从两地生产的产品中各抽取1 件,都抽到合格品的概率等于 ( )
A.112% B.9.2% C.82.8% D.0.8%
解:C
例2. 箱内有大小相同的20个红球,80个黑球,从中任意取出1个,记录它的颜色后再放回箱内,进行搅拌后再任意取出1个,记录它的颜色后又放回,假设三次都是这样抽取,试回答下列问题:
①求事件A:“第一次取出黑球,第二次取出红球,第三次取出黑球”的概率;
②求事件B:“三次中恰有一次取出红球”的概率.
解:(① 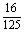 ;②
;② 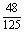
变式训练2:从甲袋中摸出一个红球的概率是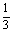 ,从乙袋中摸出1 个红球的概率是
,从乙袋中摸出1 个红球的概率是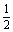 ,从两袋中各摸出1个球,则
,从两袋中各摸出1个球,则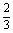 等于 ( )
等于 ( )
A.2个球不都是红球的概率
B.2个球都是红球的概率
C.至少有1个红球的概率
D.2个球中恰好有1个红球的概率
解:C
例3. 两台雷达独立工作,在一段时间内,甲雷达发现飞行目标的概率是0.9,乙雷达发现目标的概率是0.85,计算在这一段时间内,下列各事件的概率:
(1)甲、乙两雷达均未发现目标;
(2)至少有一台雷达发现目标;
(3)至多有一台雷达发现目标
解:①0.015; ②0.985; ③0.235
变式训练3:甲、乙、丙三人分别独立解一道题,甲做对的概率为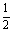 ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是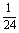 ,甲、乙、丙三人全做错的概率是
,甲、乙、丙三人全做错的概率是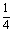 .
.
(1)求乙、丙两人各自做对这道题的概率;
(2)求甲、乙、丙三人中恰有一人做对这一道题的概率.
解: ①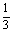 ,
,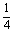 或
或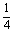 ,
,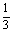 ;②
;②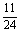
例4. 有三种产品,合格率分别为0.90,0.95和0.95,各取一件进行检验.
(1)求恰有一件不合格的概率;
(2)求至少有两件不合格的概率.(精确到0.01)
解:设三种产品各取一件,抽到的合格产品的事件分别为A、B和C
(Ⅰ)因为事件A、B、C相互独立,恰有一件不合格的概率为
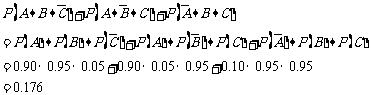
答:恰有一件不合格的概率为0.176.
(Ⅱ)解法一:至少有两件不合格的概率为
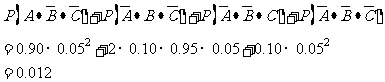
答:至少有两件不合格的概率为0.012.
解法二:三件都合格的概率为:
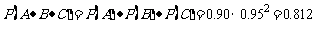
由(Ⅰ)可知恰好有一件不合格的概率为0.176,所以至少有两件不合格的概率为
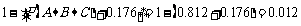 答:至少有两件不合格的概率为0.012.
答:至少有两件不合格的概率为0.012.
变式训练4. 甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为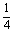 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为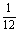 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为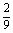 .①分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;②从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
.①分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;②从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
|
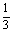 ,
,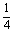 ,
,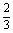 ;②
;②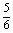
3.两个相互独立事件A,B同时发生的概率,等于每个事件发生的概率的积,即P(A·B)
=
一般地,如果事件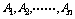 相互独立,那么:P(A1·A2……An)= .
相互独立,那么:P(A1·A2……An)= .
2.设A,B是两个事件,则A·B表示这样一个事件:它的发生,表示事件A,B ,类似地可以定义事件A1·A2·……An.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com