
1.理解空间向量的概念;掌握空间向量的加法、减法和数乘.
1.数学期望与方差,标准差都是离散型随机变量最重要的数字特征,它们分别反映了随机变量取值的平均水平、稳定程度、集中与离散的程度.离散型随机变量的期望与方差都与随机变量的分布列紧密相连,复习时应重点记住以下重要公式与结论:
一般地,若离散型随机变量 的分布列为
的分布列为
|
… |
 |
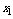 |
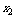 |
… |
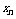 |
… |
|
… |
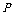 |
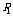 |
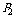 |
… |
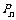 |
… |
则期望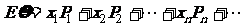 ,
,
方差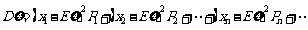 ,
,
标准差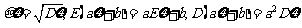
若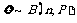 ,则
,则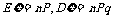 ,这里
,这里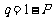
4.数学期望与方差的性质:若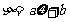 (
(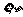 为随机变量),则
为随机变量),则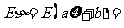 ,
,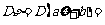 .
.
|
 的期望与方差:若
的期望与方差:若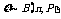 , 则
, 则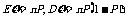
例1. 从4名男生和2名女生中任选3人参加演讲比赛,设随机变量 表示所选3人中女生的人数.
表示所选3人中女生的人数.
①求 的分布列;
的分布列;
②求 的数学期望;
的数学期望;
③求“所选3人中女生人数 ≤1”的概率.
≤1”的概率.
解:①
 |
0 |
1 |
2 |
|
P |
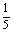 |
 |
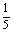 |
②E =1
=1
③
变式训练1:如果袋中有6个红球,4个白球,从中任取1球,记住颜色后放回,连续摸取4次,设 为取得红球的次数,则
为取得红球的次数,则 的期望
的期望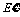 = ( )
= ( )
A.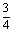 B.
B.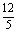
C.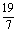 D.
D.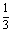
解:B
例2 抛掷两个骰子,当至少有一个5点或6点出现时,就说这次试验成功,求在30次试验中成功次数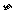 的期望和方差.
的期望和方差.
解: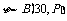 ,其中
,其中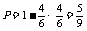 .所以
.所以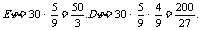
变式训练2:布袋中有大小相同的4只红球,3只黑球,今从袋中随机取出4只球,设取到一只红球得1分,取到一只黑球得3分,试求得分 的概率分布和数学期望.
的概率分布和数学期望.
解: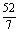
例3 甲、乙两名射手在同一条件下进行射击,分布列如下表:
射手甲
击中环数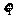 |
8 |
9 |
10 |
概率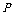 |
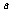 |
0.6 |
0.2 |
射手乙
击中环数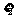 |
8 |
9 |
10 |
概率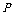 |
0.4 |
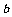 |
0.4 |
用击中环数的期望与方差分析比较两名射手的射击水平.
解: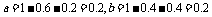
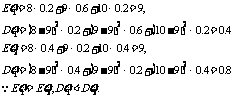
∴甲乙两名射手所得环数的平均值相等,但射手甲所得环数比较集中,射手乙所得环数比较分散,射手甲射击水平较稳定.
变式训练3:某商场根据天气预报来决定节日是在商场内还是在商场外开展促销活动,统计资料表明,每年五一节商场内的促销活动可获得经济效益2.5万元,商场外的促销活动如果不遇到有雨天可获得经济效益12万元,如果促销活动遇到有雨天,则带来经济损失5万元,4月30号气象台预报五一节当地有雨的概率是40%,问商场应该采取哪种促销方式?
解:采用场外促销方式
例4 某突发事件,在不采取任何预防措施的情况下发生的概率为0.3,一旦发生,可造成400万元的损失,现有甲、乙两种相互独立的预防措施可供采用.单独采用甲、乙预防措施所需的费用分别为45万元和30万元,采用相应预防措施后,此突发事件不发生的概率分别为0.9和0.85.若预防方案允许甲、乙两种预防措施单独采用,联合采用或不采用,试确定预防方案使总费用最少.(总费用=采取预防措施的费用+发生突发事件损失的期望值).
解:联合甲、乙,总费用最少为81万元
变式训练4:假设1部机器在1天内发生故障的概率为0.2,机器发生故障时,全天停止工作,若1周的5个工作日里无故障,可获得利润10万元,发生1次故障仍可获得利润5万元;发生2次故障所获利润为0;发生3次或3次以上故障就要亏损2万元,求1周的期望利润是多少?(精确到0.001).
解:用随机变量 表示1周5天内发生故障的天数,则
表示1周5天内发生故障的天数,则 服从地一项分布
服从地一项分布 ~B(5,0.2),
~B(5,0.2),
从而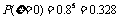 ,
,
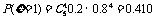 ,P(
,P( =2)=0.205
=2)=0.205
P( ≥3)=0.057设
≥3)=0.057设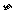 为所获得利润,则
为所获得利润,则
E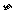 =10×0.328+5×0.410+0×0.205-2×0.057
=10×0.328+5×0.410+0×0.205-2×0.057
=5.215(万元)
|
3.数学期望与方差产生的实际背景与初中平均数及样本方差这两个概念有关.
平均数: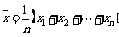
=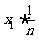 +
+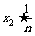 +…
+…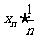
样本方差: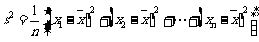
=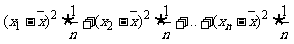
以上两式中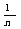 恰是
恰是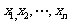 出现的频率.这与数学期望与方差的定义式一致.
出现的频率.这与数学期望与方差的定义式一致.
2.对于随机变量 ,称
,称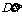
为 的方差.
的方差.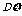 的算术平方根
的算术平方根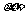 叫做
叫做 的标准差.随机变量
的标准差.随机变量 的方差与标准差都反映了随机变量取值的
.
的方差与标准差都反映了随机变量取值的
.
1.若离散型随机变量 的分布列为
的分布列为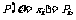
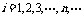 .则称
.则称 为
为 的数学期望.它反映了离散型随机变量取值的平均水平.
的数学期望.它反映了离散型随机变量取值的平均水平.
4.解决概率问题要注意“三个步骤,一个结合”:
(1)求概率的步骤是:
|
第二步,判断事件的运算,即是至少有一个发生,还是同时发生,分别运用相加或相乘事件.
第三步,运用公式求得.
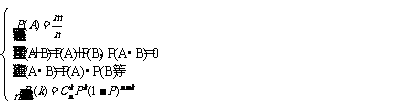
(2)概率问题常常与排列组合问题相结合.
第4课时 离散型随机变量的期望与方差
|
3.独立重复试验是指在同样条件下可重复进行的,各次之间相互独立的一种试验,每次试验都只有两重结果(即某事件要么发生,要么不发生),并且在任何一次试验中,事件发生的概率均相等.
独立重复试验是相互独立事件的特例(概率公式也是如此),就像对立事件是互斥事件的特例一样,只是有“恰好”字样的用独立重复试验的概率公式计算更简单,就像有“至少”或“至多”字样的题用对立事件的概率公式计算更简单一样.
2.运用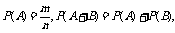 P(A·B)=P(A)·P(B)等概率公式时,应特别注意各自成立的前提条件,切勿混淆不清.例如,当
P(A·B)=P(A)·P(B)等概率公式时,应特别注意各自成立的前提条件,切勿混淆不清.例如,当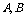 为相互独立事件时,运用公式
为相互独立事件时,运用公式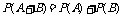 便错.
便错.
1.本节综合性强,涉及的概念、公式较多,学习时应准确理解这些概念、公式的本质内涵,注意它们的区别与联系.例如,若独立重复试验的结果只有两种(即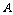 与
与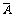 ,
,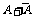 是必然事件),在
是必然事件),在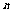 次独立重复试验中,事件
次独立重复试验中,事件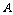 恰好发生
恰好发生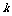 次的概率
次的概率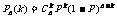 就是二项式
就是二项式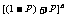 展开式中的第
展开式中的第 项,故此公式称为二项分布公式;又如两事件
项,故此公式称为二项分布公式;又如两事件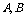 的概率均不为0,1时,“若
的概率均不为0,1时,“若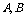 互斥,则
互斥,则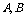 一定不相互独立”、“若
一定不相互独立”、“若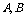 相互独立,则
相互独立,则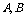 一定不互斥”等体现了不同概念、公式之间的内在联系.
一定不互斥”等体现了不同概念、公式之间的内在联系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com