
1.处理充分、必要条件问题时,首先要分清条件与结论,然后才能进行推理和判断.不仅要深刻理解充分、必要条件的概念,而且要熟知问题中所涉及到的知识点和有关概念.
4.A:圆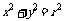 与直线
与直线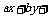
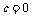 相切,B:
相切,B: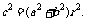
分析:要判断A是B的什么条件,只要判断由A能否推出B和由B能否推出A即可.
解:(1) 当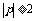 ,取
,取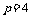 ,则方程
,则方程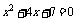 无实根;若方程
无实根;若方程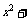
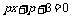 有实根,则由
有实根,则由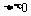 推出
推出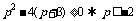 或
或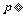 6,由此可推出
6,由此可推出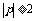 .所以A是B的必要非充分条件.
.所以A是B的必要非充分条件.
(2)若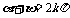 则
则


所以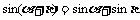 成立
成立
若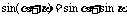 成立 取
成立 取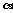
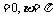 ,知
,知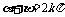 不一定成立,
不一定成立,
故A是B的充分不必要条件.
(3) 由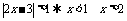 ,由
,由 解得
解得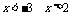 ,所以A推不出B,但B可以推出A,故A是B的必要非充分条件.
,所以A推不出B,但B可以推出A,故A是B的必要非充分条件.
(4) 直线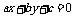 与圆
与圆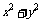
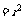 相切
相切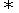 圆(0,0)到直线的距离
圆(0,0)到直线的距离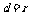 ,即
,即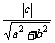 =
=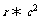 =
= .所以A是B的充要条件.
.所以A是B的充要条件.
变式训练1:指出下列命题中,p是q的什么条件(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要条件”中选出一种作答).
(1)在△ABC中,p:∠A=∠B,q:sinA=sinB;
(2)对于实数x、y,p:x+y≠8,q:x≠2或y≠6;
(3)非空集合A、B中,p:x∈A∪B,q:x∈B;
(4)已知x、y∈R,p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0.
解: (1)在△ABC中,∠A=∠B sinA=sinB,反之,若sinA=sinB,因为A与B不可能互补(因为三角形三个内角和为180°),所以只有A=B.故p是q的充要条件.
sinA=sinB,反之,若sinA=sinB,因为A与B不可能互补(因为三角形三个内角和为180°),所以只有A=B.故p是q的充要条件.
(2)易知:  p:x+y=8,
p:x+y=8,  q:x=2且y=6,显然
q:x=2且y=6,显然 q
q
 p.但
p.但 p
p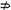
 q,即
q,即 q 是
q 是 p 的充分不必要条件,根据原命题和逆否命题的等价性知,p是q的充分不必要条件.
p 的充分不必要条件,根据原命题和逆否命题的等价性知,p是q的充分不必要条件.
(3)显然x∈A∪B不一定有x∈B,但x∈B一定有x∈A∪B,所以p是q的必要不充分条件.
(4)条件p:x=1且y=2,条件q:x=1或y=2,
所以p q但q
q但q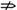 p,故p是q的充分不必要条件.
p,故p是q的充分不必要条件.
例2. 已知p:-2<m<0,0<n<1;q:关于x的方程x2+mx+n=0有两个小于1的正根,试分析p是q的什么条件.
解:若方程x2+mx+n=0有两个小于1的正根,设为x1、x2.
则0<x1<1、0<x2<1,∵x1+x2=-m,x1x2=n
∴0<-m<2,0<n<1 ∴-2<m<0,0<n<1
∴p是q的必要条件.
又若-2<m<0,0<n<1,不妨设m=-1,n=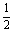 .
.
则方程为x2-x+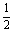 =0,∵△=(-1)2-4×
=0,∵△=(-1)2-4×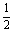 =-1<0. ∴方程无实根 ∴p是q的非充分条件.
=-1<0. ∴方程无实根 ∴p是q的非充分条件.
综上所述,p是q的必要非充分条件.
变式训练2:证明一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
证明:充分性:若ac<0,则b2-4ac>0,且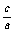 <0,
<0,
∴方程ax2+bx+c=0有两个相异实根,且两根异号,即方程有一正根和一负根.
必要性:若一元二次方程ax2+bx+c=0有一正根和一负根,则 =b2-4ac>0,x1x2=
=b2-4ac>0,x1x2=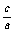 <0,∴ac<0.
<0,∴ac<0.
综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
例3. 已知p: |1- |≤2,q::x2-2x+1-m2≤0(m>0),若
|≤2,q::x2-2x+1-m2≤0(m>0),若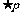 是
是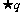 的必要而不充分条件,求实数m的取值范围.
的必要而不充分条件,求实数m的取值范围.
解: 由题意知:命题:若┒p是┑q的必要而不充分条件的等价命题即逆否命题为:p是q的充分不必要条件.
p: |1- |≤2
|≤2 -2≤
-2≤ -1≤2
-1≤2 -1≤
-1≤ ≤3
≤3 -2≤x≤10
-2≤x≤10
q: x2-2x+1-m2≤0 [x-(1-m)][x-(1+m)]≤0*
[x-(1-m)][x-(1+m)]≤0*
∵p是q的充分不必要条件,
∴不等式|1- |≤2的解集是x2-2x+1-m2≤0(m>0)解集的子集.
|≤2的解集是x2-2x+1-m2≤0(m>0)解集的子集.
又∵m>0,∴不等式*的解集为1-m≤x≤1+m
∴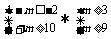 ,∴m≥9,
,∴m≥9,
∴实数m的取值范围是[9,+∞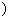
变式训练3:已知集合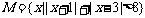 和集合
和集合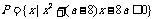 ,求a的一个取值范围,使它成为
,求a的一个取值范围,使它成为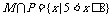 的一个必要不充分条件.
的一个必要不充分条件.
解: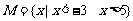 ,
,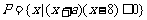
由
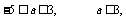
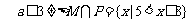
所以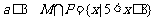 是必要但不充分条件. 说明:此题答案不唯一.
是必要但不充分条件. 说明:此题答案不唯一.
例4. “函数y=(a2+4a-5)x2-4(a-1)x+3的图象全在x轴的上方”,这个结论成立的充分必要条件是什么?
解:函数的图象全在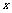 轴上方,若
轴上方,若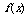 是一次函数,则
是一次函数,则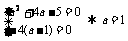
若函数是二次函数,则: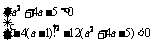
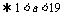
反之若 ,由以上推导,函数的图象在
,由以上推导,函数的图象在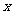 轴上方,综上,充要条件是
轴上方,综上,充要条件是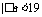 .
.
变式训练4:已知P={x | |x-1| | >2},S={x | x2+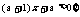 ,
, 的充要条件是
的充要条件是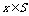 ,求实数
,求实数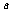 的取值范围.
的取值范围.
分析: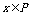 的充要条件是
的充要条件是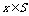 ,即任取
,即任取
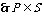 ,反过来,任取
,反过来,任取
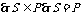 据此可求得
据此可求得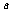 的值.
的值.
解:
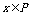 的充要条件是
的充要条件是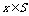
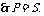 ∵P={x || x-1|>2}}=
∵P={x || x-1|>2}}=
S={x | x2+(a+1)x+a>0)}={x | (x+a)(x+1)>0}
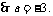
|
3.A: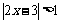 ;B:
;B: ;
;
2. A: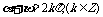 ,B:
,B: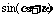
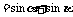 ;
;
1. A: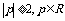 ,B:方程
,B:方程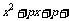
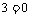 有实根;
有实根;
3.充要条件:如果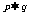 且
且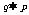 则p叫做q的
条件.
则p叫做q的
条件.
|
例1.在下列各题中,判断A是B的什么条件,并说明理由.
2.必要条件:如果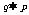 则p叫做q的
条件,q叫做p的
条件.
则p叫做q的
条件,q叫做p的
条件.
1.充分条件:如果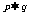 则p叫做q的
条件,q叫做p的
条件.
则p叫做q的
条件,q叫做p的
条件.
3.反证法的第一步为否定结论,需要掌握常用词语的否定(如“至少”等),而且推理过程中,一定要把否定的结论当条件用,从而推出矛盾.用反证法证明命题的一般步骤为:(1)假设命题的结论不成立,即假设命题结论的反面成立;(2)从这个假设出发,经过正确的推理论证得出矛盾;(3)由矛盾判断假设不正确,从而肯定所证命题正确.
第2课时 充要条件
|
2.当一个命题直接证明出现困难时,通常采用间接证明法,反证法就是一种间接证法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com