3．会用样本平均数估计总体期望，会用样本的方差、标准差估计总体方差、标准差．

“统计”这一章，是初中数学中的“统计初步”的深化和拓展．要求主要会用随机抽样，分层抽样的方法从总体中抽取样本，并用样本频率分布估计总体分布．本章高考题以基本题(中、低档题)为主，每年只出一道填空题，常以实际问题为背景，综合考查学生应用基础知识解决实际问题的能力．高考的热点是总体分布的估计和抽样方法．知识的交汇点是排列、组合、概率与统计的解答题．

2．会用样本频率分布估计总体的概率分布．

1．了解随机抽样，了解分层抽样的意义．

2．算法的特性:(1)有限性

(2)确定性

例1.给出求1+2+3+4+5的一个算法。

解：算法1

第一步：计算1+2，得到3

第二步：将第一步中的运算结果3与3相加，得到6

第三步：将第二步中的运算结果6与4相加，得到10

第四步：将第三步中的运算结果10与5相加，得到15

算法2

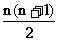第一步：取n=5

第二步：计算

第三步：输出运算结果

变式训练1.写出求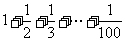的一个算法．

解：第一步：使，；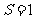

第二步：使；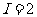

第三步：使；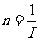

第四步：使；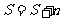

第五步：使；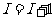

第六步：如果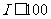，则返回第三步，否则输出．

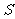例2. 给出一个判断点P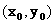是否在直线y=x-1上的一个算法。

解：第一步：将点P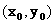的坐标带入直线y=x-1的解析式

第二步：若等式成立，则输出点P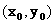在直线y=x-1上

若等式不成立，则输出点P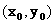不在直线y=x-1上

变式训练2.任意给定一个大于1的整数n，试设计一个程序或步骤对n是否为质数做出判断.

分析：(1)质数是只能被1和自身整除的大于1的整数.

(2)要判断一个大于1的整数n是否为质数，只要根据质数的定义，用比这个整数小的数去除n，如果它只能被1和本身整除，而不能被其它整数整除，则这个数便是质数.

解：算法：第一步：判断n是否等于2.若n=2，则n是质数；若n＞2，则执行第二步.

第二步：依次从2~(n-1)检验是不是n的因数，即整除n的数.若有这样的数，则n不是质数；若没有这样的数，则n是质数.

例3. 解二元一次方程组：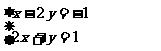　

分析：解二元一次方程组的主要思想是消元的思想，有代入消元和加减消元两种消元的方法，下面用加减消元法写出它的求解过程.

解：第一步：② - ①×2，得： 5y=3；　　　 ③

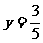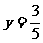第二步：解③得 ；　　　　　 第三步：将代入①，得 .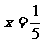

变式训练3.设计一个算法，使得从10个确定且互不相等的数中挑选出最大的一个数.

解：算法1

第一步：假定这10个数中第一个是“最大值”；

第二步：将下一个数与“最大值”比较，如果它大于此“最大值”，那么就用这个数取代“最大值”，否则就取“最大值”；

第三步：再重复第二步。

第四步：在这十个数中一直取到没有可以取的数为止，此时的“最大值”就是十个数中的最大值。

算法2

第一步：把10个数分成5组，每组两个数，同组的两个数比较大小，取其中的较大值；

第二步：将所得的5个较大值按2，2，1分组，有两个数的组组内比较大小，一个数的组不变；

第三步：从剩下的3个数中任意取两个数比较大小，取其中较大值，并将此较大值与另一个数比较，此时的较大值就是十个数中的最大值。

例4. 用二分法设计一个求方程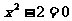的近似根的算法.

分析：该算法实质是求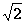的近似值的一个最基本的方法.

解：设所求近似根与精确解的差的绝对值不超过0.005，算法：

第一步：令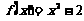.因为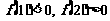，所以设x₁=1，x₂=2.

第二步：令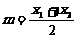，判断f(m)是否为0.若是，则m为所求；若否，则继续判断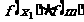大于0还是小于0.

第三步：若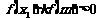，则x₁=m；否则，令x₂=m.

第四步：判断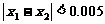是否成立？若是，则x₁、x₂之间的任意值均为满足条件的近似根；若否，则返回第二步.

变式训练4.一个人带三只狼和三只羚羊过河，只有一条船，同船可以容纳一个人和两只动物．没有人在的时候，如果狼的数量不少于羚羊的数量，狼就会吃掉羚羊．请设计过河的算法．

解：算法或步骤如下：

S1　 人带两只狼过河；

S2　 人自己返回；

S3　 人带一只羚羊过河；

S4　 人带两只狼返回；

S5　 人带两只羚羊过河；

S6　 人自己返回；

S7　 人带两只狼过河；

S8　 人自己返回；

S9　 人带一只狼过河．

第2课时　 　程序框图

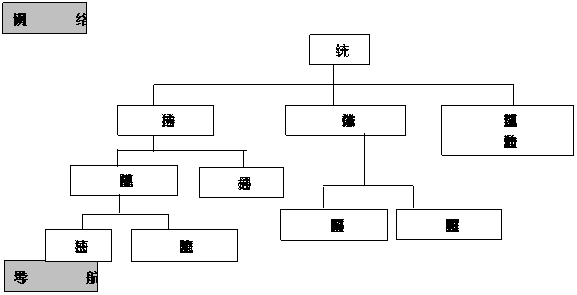
(1)程序构图的概念：程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。

一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明。

(2)构成程序框的图形符号及其作用

程序框	名称	功能
	起止框	表示一个算法的起始和结束，是任何流程图不可少的。
	输入、输出框	表示一个算法输入和输出的信息，可用在算法中任何需要输入、输出的位置。
	处理框	赋值、计算，算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内。
	判断框	判断某一条件是否成立，成立时在出口处标明“是”或“Y”；不成立时标明“否”或“N”。

学习这部分知识的时候，要掌握各个图形的形状、作用及使用规则，画程序框图的规则如下：

算法不仅是数学及其应用的重要组成部分，也是计算机科学的重要基础。算法初步虽然是新课标增加的内容，但与前面的知识有着密切的联系，并且与实际问题的联系也非常密切。因此，在高考中算法初步知识将与函数、数列、三角、概率、实际问题等知识点进行整合，是高考试题命制的新“靓”点。这样试题就遵循了“在知识网络交汇处设计试题”的命制原则，既符合高考命题“能力立意”的宗旨，又突出了数学的学科特点。这样做，可以从学科的整体高度和思维价值的高度考虑问题，可以揭示数学各知识之间得到的内在联系，可以使考查达到必要的深度。

考查形式与特点是：

(1)选择题、填空题主要考查算法的含义、流程图、基本算法语句等内容，一般在每份试卷中有1-2题，多为中档题出现。

(2)在解答题中可通过让学生读程序框图去解决其它问题，此类试题往往是与数列题结合在一起，具有一定的综合性，可以考查学生的识图能力及对数列知识的掌握情况.

第1课时　　 算法的含义

1．算法的概念:对一类问题的机械的、统一的求解方法称为算法。

5．对一个命题而言，使结论成立的充分条件可能不止一个，必要条件也可能不止一个．

4．对于充要条件的证明题，既要证明充分性，又要证明必要性，从命题角度出发，证原命题为真，逆命题也为真；求结论成立的充要条件可以从结论等价变形(换)而得到，也可以从结论推导必要条件，再说明具有充分性．

3．等价变换是判断充分、必要条件的重要手段之一，特别是对于否定的命题，常通过它的等价命题，即逆否命题来考查条件与结论间的充分、必要关系．

2．确定条件为不充分或不必要的条件时，常用构造反例的方法来说明．