
4.避免重复和遗漏.
第4课时 排列组合综合题
|
3.组合问题的一般可抽象为“选派”模型来处理.另外有的问题也可用框图结合对应思想来处理。
2.要注意准确理解“有且仅有” “至多”“至少”“全是”“都不是”“不都是”等词语的确切含义.
1.解有关组合应用问题时,首先要判断这个问题是不是组合问题.区别组合问题和排列问题的唯一标准是“顺序”.需要考虑顺序的是排列问题不需要考虑顺序的的才是组合问题.
3.组合数性质:
①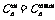
②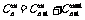
③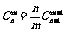
④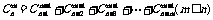
⑤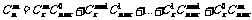
|
例1. 某培训班有学生15名,其中正副班长各一名,先选派5名学生参加某种课外活动.
(1) 如果班长和副班长必须在内有多少种选派法.
(2) 如果班长和副班长有且只有1人在内有多少种派法.
(3) 如果班长和副班长都不在内有多少种派法.
(4) 如果班长和副班长至少有1人在内,有多少种派法.
解;(1) 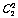
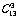 =286 (2)
=286 (2) 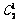
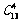 =1430 (3)
=1430 (3) 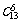 =1287
=1287
(4) 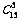 -
-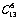 =1716
=1716
变式训练1:从4名男生和3名女生中选4人参加某个座谈会,若这4个人中必须既有男生又有女生,则不同的选法有 ( )
A.140 B.120
C.35 D.34
解:D
例2. 从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中至少有1名女生,则选派方案共有( )
A、108种 B、186种 C.216种 D、270种
解:没有女生的选法有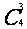 , 至少有1名女生的选法有
, 至少有1名女生的选法有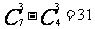 种,
种,
所以选派方案总共有:31×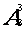 =186种。
故选B.
=186种。
故选B.
变式训练2:从5位男教师和4位女教师中选出3位教师派到3个班担任班主任(每班一位班主任),要求这3位班主任中男女教师都要有,则不同的选派方案共有 ( )
A.210种 B.420种
C.630种 D.840种
解:B
例3. (1) 把10本相同的书分给编号1,2,3的阅览室,要求每个阅览室分得的书数不大于其编号数,则不同的分法有多少种?
(2) 以平行六面体ABCD-A1B1C1D21的任意三个点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面情况有多少种?
(3) 一次文艺演出中需要给舞台上方安装一排完全相同的彩灯15只,现以不同的亮灯方式来增加舞台效果,设计者按照每次亮灯时恰好有6只是关的,且相邻的灯不能同时关掉,两端的灯必须要亮的要求进行设计,求有多少不同的亮灯方式?
解:(1)先在编号为1,2,3的阅览室中依次放入0,1,2本书,再用隔板法分配剩下的书有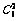 =15种,(2)平行六面体中能构成三角形个数
=15种,(2)平行六面体中能构成三角形个数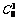 =56为任取两个有
=56为任取两个有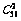 种情况,其中共面的有12
种情况,其中共面的有12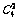 ,因而不共面的有
,因而不共面的有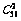 -12
-12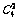 种 (3)
种 (3)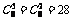
变式训练3:马路上有编号为1, 2, 3, 4…..10的十盏路灯,为节约用电,又不影响照明可以把其中的三盏关掉,但不能关掉相邻的两盏,也不能关掉两端的路灯,则满足条件的关灯方法种数有_______种.
解:20 用插排法,把七盏亮灯排成一排,七盏亮灯之间有6个间隔,再将三盏不亮的灯插入其中的3个间隔,一种插法对应一种关灯的方法,故有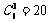 种关灯方法.
种关灯方法.
例4. 四面体的顶点和各棱中点共有10个点,
(1) 在其中取4个共面的点,共有多少种不同的取法?
(2) 在其中取4个不共面的点,共有多少种不同的取法.
解:(1)四个点共面的取法可分三类.第一类:再同一个面上取,共有4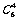 个面;第二类:在一条棱上取三点,再在它所对的棱上取中点,共有6个面;第三类:在六条棱的六个中点中取,取两对对棱的4个中点,共有
个面;第二类:在一条棱上取三点,再在它所对的棱上取中点,共有6个面;第三类:在六条棱的六个中点中取,取两对对棱的4个中点,共有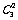 =3个面.故有69种.
=3个面.故有69种.
(2) 用间接法.共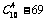 =141个面.
=141个面.
变式训练4:在1, 2, 3…100这100个数中任选不同的两个数,求满足下列条件时各有多少种不同的取法.
(1) 其和是3的倍数
(2) 其差是3的倍数(大数减小数).
(3) 相加,共有多少个不同的和.
(4) 相乘,使其积为7的倍数.
解:(1) 1650 (2) 1617 (3) 197 (4)1295
|
2.排列与组合的共同点,就是都要“从n个不同元素中,任取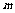 个元素”,而不同点就是前者要“按一定的顺序成一列”,而后者却是“不论怎样的顺序并成一组”.
个元素”,而不同点就是前者要“按一定的顺序成一列”,而后者却是“不论怎样的顺序并成一组”.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号Cmn表示.
组合数公式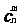 =
=
=
=
在求具体的组合数时,常用上面的公式,分子由连续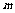 个自然数之积,最大的数为
个自然数之积,最大的数为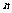 ,最小的数是
,最小的数是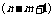 ,分母是
,分母是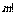 ,如果进行抽象的证明时,一般常用下面的公式
,如果进行抽象的证明时,一般常用下面的公式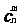 = ,它的分子是
= ,它的分子是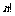 ,分母是
,分母是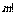 与
与 的积.
的积.
1.一般地说,从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
4.由于排列问题的结果一般数目较大.不易直接验证,解题时要深入分析,严密周详,要防止重复和遗漏.为此可用多种不同的方法求解看看结果是否相同.
第3课时 组 合
|
3.解排列应用问题思路一定要清晰,并随时注意转换解题角度,通过练习要认真理会解排列问题的各种方法.
2.解有约束条件的排列问题的几种策略.
a. 特殊元素,特殊位置优先定位(也有个别例外情况,见例1)
b. 相邻问题捆绑处理不相邻问题插空处理
c. 正难则反,等价转换
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com