
3.补集:集合A是集合S的子集,由
的元素组成的集合,叫做S中子集A的补集,记作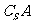 ,即
,即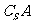 =
.
=
.
2.并集:由 的元素组成的集合,叫做集合A与B的并集,记作A∪B,即A∪B= .
1.交集:由 的元素组成的集合,叫做集合A与B的交集,记作A∩B,即A∩B= .
4.要注意数学思想方法在解题中的运用,如化归与转化、分类讨论、数形结合的思想方法在解题中的应用.
第2课时 集合的运算
|
3.注意空集φ的特殊性,在解题时,若未指明集合非空,则要考虑到集合为空集的可能性.
2.利用相等集合的定义解题时,特别要注意集合中元素的互异性,对计算的结果要加以检验.
10.空集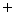 是一个特殊而又重要的集合,它不含任何元素,
是一个特殊而又重要的集合,它不含任何元素,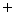 是任何集合的
,
是任何集合的
,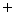 是任何非空集合的
,解题时不可忽视
是任何非空集合的
,解题时不可忽视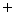 .
.
|
例1. 已知集合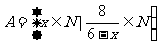 ,试求集合
,试求集合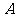 的所有子集.
的所有子集.
解:由题意可知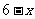 是
是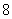 的正约数,所以
的正约数,所以 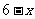 可以是
可以是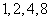 ;相应的
;相应的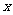 为
为
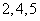 ,即
,即 .
.
∴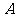 的所有子集为
的所有子集为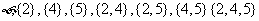 .
.
变式训练1.若a,b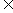 R,集合
R,集合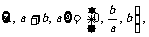 求b-a的值.
求b-a的值.
解:由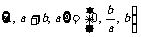 可知a≠0,则只能a+b=0,则有以下对应关系:
可知a≠0,则只能a+b=0,则有以下对应关系:
 ①或
①或 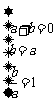 ②
②
由①得 符合题意;②无解.所以b-a=2.
符合题意;②无解.所以b-a=2.
例2. 设集合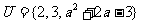 ,
,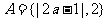 ,
,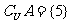 ,求实数a的值.
,求实数a的值.
解:此时只可能 ,易得
,易得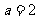 或
或 。
。
当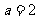 时,
时,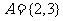 符合题意。
符合题意。
当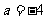 时,
时,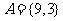 不符合题意,舍去。
不符合题意,舍去。
故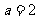 。
。
变式训练2:(1)P={x|x2-2x-3=0},S={x|ax+2=0},S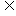 P,求a取值?
P,求a取值?
(2)A={-2≤x≤5},B={x|m+1≤x≤2m-1},B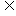 A,求m。
A,求m。
解:(1)a=0,S=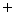 ,
,
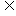 P成立 a
P成立 a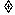 0,S
0,S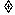
 ,由S
,由S P,P={3,-1}
P,P={3,-1}
得3a+2=0,a=-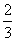 或-a+2=0,a=2; ∴a值为0或-
或-a+2=0,a=2; ∴a值为0或-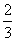 或2.
或2.
(2)B=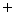 ,即m+1>2m-1,m<2 ∴
,即m+1>2m-1,m<2 ∴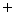
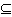 A成立.
A成立.
B≠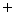 ,由题意得
,由题意得 得2≤m≤3
得2≤m≤3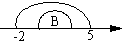
∴m<2或2≤m≤3 即m≤3为取值范围.
注:(1)特殊集合 作用,常易漏掉
作用,常易漏掉
例3. 已知集合A={x|mx2-2x+3=0,m∈R}.
(1)若A是空集,求m的取值范围;
(2)若A中只有一个元素,求m的值;
(3)若A中至多只有一个元素,求m的取值范围.
解: 集合A是方程mx2-2x+3=0在实数范围内的解集.
(1)∵A是空集,∴方程mx2-2x+3=0无解.
∴Δ=4-12m<0,即m>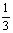 .
.
(2)∵A中只有一个元素,
∴方程mx2-2x+3=0只有一个解.
若m=0,方程为-2x+3=0,只有一解x= ;
;
若m≠0,则Δ=0,即4-12m=0,m=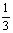 .
.
∴m=0或m=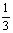 .
.
(3)A中至多只有一个元素包含A中只有一个元素和A是空集两种含义,根据(1)、(2)的结果,
得m=0或m≥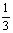 .
.
变式训练3.(1)已知A={a+2,(a+1)2,a2+3a+3}且1∈A,求实数a的值;
(2)已知M={2,a,b},N={2a,2,b2}且M=N,求a,b的值.
解:(1)由题意知:
a+2=1或(a+1)2=1或a2+3a+3=1,
∴a=-1或-2或0,根据元素的互异性排除-1,-2, ∴a=0即为所求.
(2)由题意知,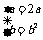 或
或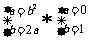 或
或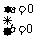 或
或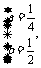
根据元素的互异性得 或
或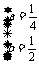 即为所求.
即为所求.
例4. 若集合A={2,4,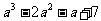 },B={1,a+1,
},B={1,a+1,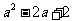 ,
,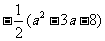 、
、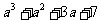 },且A∩B={2,5},试求实数
},且A∩B={2,5},试求实数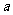 的值.
的值.
解:∵А∩В={2,5},∴2∈A且5∈A,
则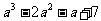 =5
=5 (a-2)(a-1)(a+1)=0,
(a-2)(a-1)(a+1)=0,
∴a=-1或a=1或a=2.
当a=-1时,B={1,0,5,2,4},与A∩B={2,5}矛盾,∴a≠-1.
当a=1时,B={1,2,1,5,12},与集合中元素互异性矛盾,∴a≠1.
当a=2时,B={1,3,2,5,25},满足A∩B={2,5}.故所求a的值为2.
变式训练4.已知集合A={a,a+d,a+2d},B={a,aq,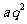 },其中a≠0,若A=B,求q的值
},其中a≠0,若A=B,求q的值
解:∵A=B
∴(Ⅰ)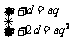 或 (Ⅱ)
或 (Ⅱ) 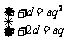
由(Ⅰ)得q=1,由(Ⅱ)得q=1或q=-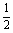 .
.
当q=1时,B中的元素与集合元素的互异性矛盾,
∴q=-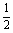
|
|
9.若集合A含有n个元素,则A的子集有 个,真子集有 个,非空真子集有 个.
8.真子集:如果 就说集合A是集合B的真子集,记作 .
7.相等:若集合A中 都是集合B的元素,同时集合B中 都是集合A的元素,就说集合A等于集合B,记作 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com