
(2009·全国卷Ⅱ)近期研制出利用玉米叶片加工、编织购物袋的技术,这种购物袋易分解且物美价廉。据此完成6-7题。
6.该种购物袋的生产厂应接近 ( )
A.原料产地 B.销售市场
C.能源基地 D.研发基地
解析:购物袋利用了玉米叶片加工,制成品重量、体积大大减小,因此生产厂应接近原料产地。
答案:A
7.以该种购物袋替代目前广泛使用的同类用品,对环境保护的直接作用是 ( )
A.减轻大气污染 B.减轻“白色污染”
C.促进生物多样性 D.减轻酸雨危害
解析:目前购物袋使用的原料是化工产品,易造成“白色污染”,使用易分解的生物原料产品,对环境保护的直接作用是减轻“白色污染”。
答案:B
2009年上海动漫娱乐展于7月3日至6日在上海展览中心隆重举行。动漫产业是个需要大量专业人才的产业。目前,动漫产业已经成为日本第三大产业。根据材料,回答4-5题。
4.根据材料中的信息判断,动漫产业属于 ( )
A.劳动力导向型 B.技术导向型
C.原料导向型 D.市场导向型
解析:根据题中的信息可知,动漫产业对技术的要求较高,属于技术导向型。
答案:B
5.日本是世界上的动漫产业大国,下列叙述正确的是 ( )
A.日本是个四面临海的岛国,有利于动漫产业的出口
B.日本的钢铁工业发达,为动漫产业的发展提供了坚实的物质基础
C.日本科技水平高,动漫设计人员多且素质高
D.日本的人口稠密,劳动力廉价,许多人员靠设计动漫维持生计
解析:日本是一个发达国家,对教育非常重视,因此科技水平较高,而动漫产业属技术导向型,适宜分布在科技水平高的地区。
答案:C
3.对于给出集合是否为空集,集合中的元素个数是否确定,都是常见的讨论点,解题时要有分类讨论的意识.
2.集合的运算可以用韦恩图帮助思考,实数集合的交、并运算可在数轴上表示,注意在运算中运用数形结合思想.
1.在解决有关集合运算题目时,关键是准确理解题目中符号语言的含义,善于转化为文字语言.
4.A∪B=A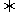
A∩B=A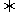
|
例1. 设全集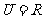 ,
,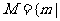 方程
方程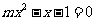 有实数根
有实数根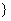 ,
,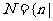 方程
方程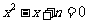
有实数根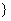 ,求
,求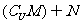 .
.
解:当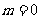 时,
时,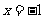 ,即
,即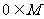 ;
;
当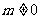 时,
时, 即
即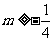 ,且
,且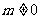 ∴
∴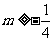 ,
,
∴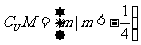
而对于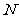 ,
,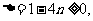 即
即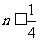 ,∴
,∴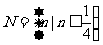 .
.
∴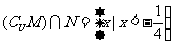
变式训练1.已知集合A=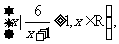 B=
B=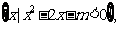
(1)当m=3时,求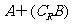 ;
;
(2)若A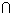 B
B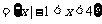 ,求实数m的值.
,求实数m的值.
解: 由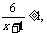 得
得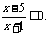 ∴-1<x≤5,∴A=
∴-1<x≤5,∴A=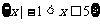 .
.
(1)当m=3时,B=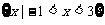 ,则
,则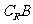 =
=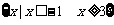 ,
,
∴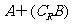 =
=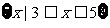 .
.
(2)∵A=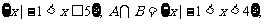 ∴有42-2×4-m=0,解得m=8.
∴有42-2×4-m=0,解得m=8.
此时B=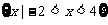 ,符合题意,故实数m的值为8.
,符合题意,故实数m的值为8.
例2. 已知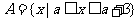 ,
,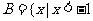 或
或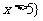 .
.
(1)若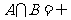 ,求
,求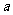 的取值范围;
的取值范围;
(2) 若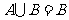 ,求
,求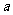 的取值范围.
的取值范围.
解:(1)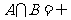 ,
∴
,
∴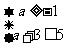 ,解之得
,解之得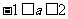 .
.
(2) 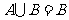 ,
∴
,
∴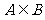 . ∴
. ∴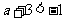 或
或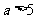 ,
, 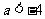 或
或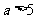
∴若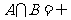 ,则
,则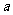 的取值范围是
的取值范围是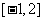 ;若
;若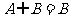 ,则
,则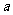 的取值范围是
的取值范围是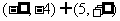 .
.
变式训练2:设集合A=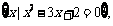 B
B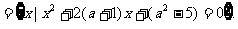
(1)若A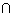 B
B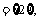 求实数a的值;
求实数a的值;
(2)若A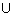 B=A,求实数a的取值范围;
B=A,求实数a的取值范围;
(3)若U=R,A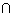 (
(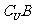 )=A.求实数a的取值范围.
)=A.求实数a的取值范围.
解:由x2-3x+2=0得x=1或x=2,故集合A=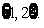
(1)∵A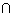 B
B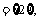 ∴2
∴2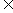 B,代入B中的方程,
B,代入B中的方程,
得a2+4a+3=0,∴a=-1或a=-3;
当a=-1时,B=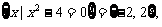 满足条件;
满足条件;
当a=-3时,B=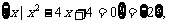 满足条件;
满足条件;
综上,a的值为-1或-3.
(2)对于集合B,
 =4(a+1)2-4(a2-5)=8(a+3).
=4(a+1)2-4(a2-5)=8(a+3).
∵A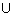 B=A,∴B
B=A,∴B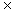 A,
A,
①当 <0,即a<-3时,B=
<0,即a<-3时,B=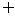 ,满足条件;
,满足条件;
②当 =0,即a=-3时,B
=0,即a=-3时,B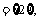 ,满足条件;
,满足条件;
③当 >0,即a>-3时,B=A=
>0,即a>-3时,B=A=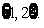 才能满足条件,
才能满足条件,
则由根与系数的关系得
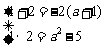 即
即 矛盾;
矛盾;
综上,a的取值范围是a≤-3.
(3)∵A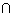 (
(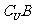 )=A,∴A
)=A,∴A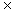
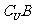 ,∴A
,∴A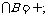
①若B=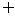 ,则
,则 <0
<0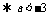 适合;
适合;
②若B≠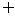 ,则a=-3时,B=
,则a=-3时,B=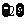 ,A
,A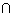 B=
B=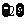 ,不合题意;
,不合题意;
a>-3,此时需1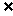 B且2
B且2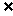 B,将2代入B的方程得a=-1或a=-3(舍去);
B,将2代入B的方程得a=-1或a=-3(舍去);
将1代入B的方程得a2+2a-2=0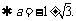
∴a≠-1且a≠-3且a≠-1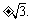
综上,a的取值范围是a<-3或-3<a<-1-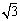 或-1-
或-1-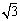 <a<-1或-1<a<-1+
<a<-1或-1<a<-1+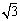 或a>-1+
或a>-1+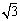 .
.
例3. 已知集合A=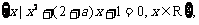 B
B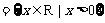 ,试问是否存在实数a,使得A
,试问是否存在实数a,使得A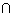 B
B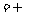 若存在,求出a的值;若不存在,请说明理由.
若存在,求出a的值;若不存在,请说明理由.
解:方法一
假设存在实数a满足条件A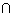 B=
B=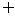 则有
则有
(1)当A≠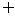 时,由A
时,由A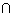 B=
B=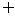 ,B
,B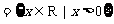 ,知集合A中的元素为非正数,
,知集合A中的元素为非正数,
设方程x2+(2+a)x+1=0的两根为x1,x2,则由根与系数的关系,得

(2)当A=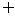 时,则有
时,则有 =(2+a)2-4<0,解得-4<a<0.
=(2+a)2-4<0,解得-4<a<0.
综上(1)、(2),知存在满足条件A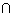 B=
B=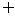 的实数a,其取值范围是(-4,+∞).
的实数a,其取值范围是(-4,+∞).
方法二 假设存在实数a满足条件A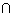 B≠
B≠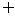 ,则方程x2+(2+a)x+1=0的两实数根x1,x2至少有一个为正,
,则方程x2+(2+a)x+1=0的两实数根x1,x2至少有一个为正,
因为x1·x2=1>0,所以两根x1,x2均为正数.
则由根与系数的关系,得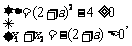 解得
解得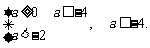
又∵集合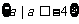 的补集为
的补集为
∴存在满足条件A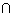 B=
B=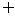 的实数a,其取值范围是(-4,+∞).
的实数a,其取值范围是(-4,+∞).
变式训练3.设集合A={(x,y)|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*},问是否存在非零整数a,使A∩B≠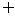 ?若存在,请求出a的值;若不存在,说明理由.
?若存在,请求出a的值;若不存在,说明理由.
解:假设A∩B≠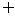 ,则方程组
,则方程组
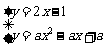 有正整数解,消去y,得ax2-(a+2)x+a+1=0.
有正整数解,消去y,得ax2-(a+2)x+a+1=0.
由Δ≥0,有(a+2)2-4a(a+1)≥0,解得-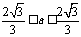 .因a为非零整数,∴a=±1,
.因a为非零整数,∴a=±1,
当a=-1时,代入(*), 解得x=0或x=-1,
而x∈N*.故a≠-1.当a=1时,代入(*),
解得x=1或x=2,符合题意.故存在a=1,使得A∩B≠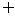 ,
,
此时A∩B={(1,1),(2,3)}.
|
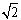 ax+a2+a+2=0,x∈R},是否存在实数a,使得A
ax+a2+a+2=0,x∈R},是否存在实数a,使得A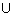 B=
B=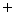 ?若存在,求出实数的值;若不存在,说明理由.
?若存在,求出实数的值;若不存在,说明理由.
解:1<a<2即实数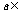 (1,2)时,
(1,2)时,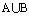 =
=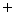 .
.
变式训练4.设集合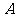 为函数
为函数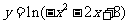 的定义域,集合
的定义域,集合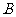 为函数
为函数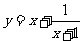 的值域,集合
的值域,集合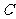 为不等式
为不等式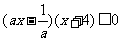 的解集.(1)求
的解集.(1)求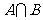 ;(2)若
;(2)若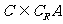 ,求
,求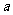 的取值范围.
的取值范围.
解:(1)解得A=(-4,2), B=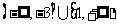 。 所以
。 所以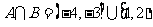
|
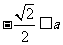 <0
<0
3.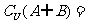 ,
,
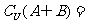 ,
,
2.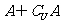 =
,
=
,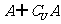 =
,
=
,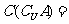 .
.
1.A∩A=
,A∩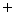 =
,A∩B=
,B∩A,A∪A=
,
=
,A∩B=
,B∩A,A∪A=
,
A∪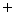 = ,A∪B=B∪A
= ,A∪B=B∪A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com