2．如图，已知平面α∥β∥γ，A，C∈α，B，D∈γ，异面直线AB和CD分别与β交于

E和G，连结AD和BC分别交β于F，H.

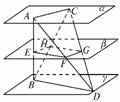
(1)求证：＝；

(2)判断四边形EFGH是哪一类四边形；

(3)若AC＝BD＝a，求四边形EFGH的周长．

解答：(1)证明：由AB，AD确定的平面，与平行平面β和γ的交线分别为EF和BD，

知EF∥BD.所以＝.同理有FG∥AC，因而＝.所以＝.

(2)面CBD分别交β，γ于HG和BD.由于β∥γ，所以HG∥BD.同理EH∥AC.故EFGH

为平行四边形．

(3)由EF∥BD，得＝＝.由FG∥AC，得＝＝.

又因为BD＝AC＝a，所以+＝＝＝1.即EF+FG＝a.

故四边形EFGH的周长为2a.

1．如果α∥β，AB和CD是夹在平面α与β之间的两条线段，AB⊥CD，且AB＝2，

直线AB与平面α所成的角为30°，那么线段CD的取值范围是(　)

A．(，]　 　　B．[1，+∞)　 　　C．[1，]　 　　D．[，+∞)

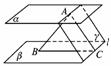
解析：如图，过A点作平面γ⊥AB，γ∩β＝l，过A作AC⊥l.

垂足为C，连结AC，可以证明AC即为线段CD的最小值．

在Rt△ABC中，∠ABC＝30°，AB＝2，

∴AC＝ABtan∠ABC＝.即CD≥.

答案：D

10．已知：如右图，平面α∥平面β，线段AB分别交α、β于点M、N，线段AD分别

交α、β于C、D，线段BF分别交α、β于F、E，且AM＝BN，试证：S_△CMF＝S_△DNE.

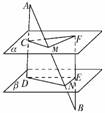
证明：∵α∥β，直线AD与AB确定的平面与α、β分别交于CM、DN，

∴CM∥DN，同理NE∥MF，∴∠CMF＝∠DNE，＝.＝，

又AM＝BN，∴＝，即CM·MF＝DN·NE，∴CM·MFsin∠CMF＝

DN·NEsin∠DNE.因此S_△CMF＝S_△DNE.

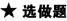
9．(原创题)如图在四面体S-ABC中，E、F、O分别为SA、SB、AC的中点，G为OC的中点，证明：FG∥平面BEO.

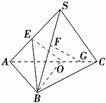
证明：证法一：如图，取BC中点M，连接FM，GM，则GM∥OB，FM∥SC∥EO，

又FM∩GM＝M，则平面FGM∥平面BEO，因此FG∥平面BEO.

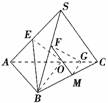
证法二：设，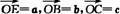

则＝＝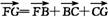

＝＝

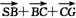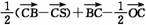
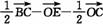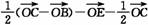
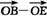＝－＝－b－a，因此FG与b，a共面，∴FG∥平面BEO.

8．如下图，在正方体ABCD-A₁B₁C₁D₁中，M、N、P、Q分别为A₁D₁、A₁B₁、B₁C₁、C₁D₁的中点，求证：平面AMN∥平面PQDB.

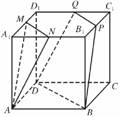
证明：如图连结NQ，由NQ綊A₁D₁綊AD知：四边形ADQN为平行四边形，则AN∥DQ；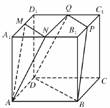

同理AM∥BP，又AM∩AN＝A，根据平面与平面平行的判定定理可知，平面AMN∥平面PQDB.

7．下列命题中正确的命题是________．

①直线l上有两点到平面α距离相等，则l∥α；

②平面α内不在同一直线上三点到平面β的距离相等，则α∥β；

③垂直于同一直线的两个平面平行；

④平行于同一直线的两平面平行；

⑤若a、b为异面直线，a⊂α，b∥α，b⊂β，a∥β，则α∥β.

答案：③⑤

6．到空间不共面的四点距离相等的平面个数为________．

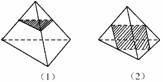
解析：如右图分类，一类如图(1)将四点视为三棱锥四个顶点，取棱中点，可以做如图(1)平面平行于三棱锥的底面，并到另一顶点距离与底面距离相等，这样的平面有4个；另一类如图(2)取各段中点，四个中点形成平面平行于三棱锥相对棱，这样的平面有3个，共7个．

答案：7

5．设α、β、γ为两两不重合的平面，l、m、n为两两不重合的直线，给出下列四个命题，其中真命题的个数是(　)

①若α⊥γ，β⊥γ，则α∥β；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；③若α∥β，l⊂α，则l∥β；④若α∩β＝l，β∩γ＝m，γ∩α＝n，l∥γ，则m∥n.

A．1　 　　　B．2 　　　　C．3　 　　　　D．4

答案：B

4．(2009·南京质检)已知平面α∥平面β，P是α、β外一点，过点P的直线m与α、β分别交于A、C，过点P的直线n与α、β分别交于B、D且PA＝6，AC＝9，PD＝8，则BD的　 长为(　)

A．16　 　　　B．24或　 　C．14　 　　D．20

解析：根据题意可出现以下如图两种情况

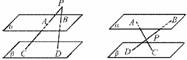
可求出BD的长分别为或24.

答案：B

3．设a、b是异面直线，下列命题正确的是(　)

A．过不在a、b上的一点P一定可以作一条直线和a、b都相交

B．过不在a、b上的一点P一定可以作一个平面和a、b都垂直

C．过a一定可以作一个平面与b垂直

D．过a一定可以作一个平面与b平行

解析：可证明过a一定有一个平面与b平行．

答案：D