
从A、B、C、D 四个选项中, 选出可以填入空白处的最佳选项,并用铅笔把答题卡上对应题目的答案标号涂黑。
第一节 单项填空(共15小题;每小题1分,满分15分)
21. --- How would you like your Cappuccino coffee?
--- ______.
A. It’s well done B. The stronger, the better.
C. One cup. That’s enough D. Very nice. Thank you.
1在△ABC中,已知B=30°,b=50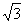 ,c=150,那么这个三角形是( )
,c=150,那么这个三角形是( )
A等边三角形 B直角三角形 C等腰三角形 D等腰三角形或直角三角形
2在△ABC中,若b2sin2C+c2sin2B=2bccosBcosC,则此三角形为( )
A直角三角形 B等腰三角形 C等边三角形 D等腰直角三角形
3在△ABC中,已知sinA∶sinB∶sinC=6∶5∶4,则secA=
4△ABC中,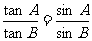 ,则三角形为
,则三角形为
5在△ABC中,角A、B均为锐角且cosA>sinB,则△ABC是
6已知△ABC中, ,试判断△ABC的形状
,试判断△ABC的形状
7在△ABC中,(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断△ABC的形状
1正余弦定理的边角互换功能
对于正、余弦定理,同学们已经开始熟悉,在解三角形的问题中常会用到它其实,在涉及到三角形的其他问题中,也常会用到它们两个定理的特殊功能是边角互换,即利用它们可以把边的关系转化为角的关系,也可以把角的关系转化为边的关系,从而使许多问题得以解决
例1已知a、b为△ABC的边,A、B分别是a、b的对角,且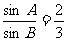 ,求
,求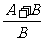 的值
的值
解:∵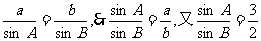 (这是角的关系),
(这是角的关系),
∴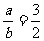 (这是边的关系)于是,由合比定理得
(这是边的关系)于是,由合比定理得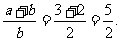
例2已知△ABC中,三边a、b、c所对的角分别是A、B、C,且a、b、c成等差数列
求证:sinA+sinC=2sinB
证明:∵a、b、c成等差数列,
∴a+c=2b(这是边的关系)①
又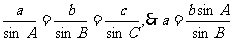 ②
②
 ③
③
将②、③代入①,得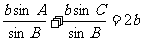 整理得sinA+sinC=2sinB(这是角的关系)
整理得sinA+sinC=2sinB(这是角的关系)
2正、余弦定理的巧用
某些三角习题的化简和求解,若能巧用正、余弦定理,则可避免许多繁杂的运算,从而使问题较轻松地获得解决,现举例说明如下:
例3求sin220°+cos280°+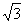 sin20°cos80°的值
sin20°cos80°的值
解:原式=sin220°+sin210°-2sin20°sin10°cos150°
∵20°+10°+150°=180°,
∴20°、10°、150°可看作一个三角形的三个内角
设这三个内角所对的边依次是a、b、c,由余弦定理得:a2+b2-2abcos150°=c2(※)
而由正弦定理知:a=2Rsin20°,b=2Rsin10°,c=2Rsin150°,代入(※)式得:
sin220°+sin210°-2sin20°sin10°cos150°=sin2150°=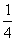
∴原式=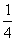
例4在△ABC中,三边长为连续的自然数,且最大角是最小角的2倍,求此三角形的三边长 (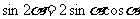 )
)
分析:由于题设条件中给出了三角形的两角之间的关系,故需利用正弦定理建立边角关系其中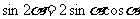 利用正弦二倍角展开后出现了cosα,可继续利用余弦定理建立关于边长的方程,从而达到求边长的目的
利用正弦二倍角展开后出现了cosα,可继续利用余弦定理建立关于边长的方程,从而达到求边长的目的
解:设三角形的三边长分别为x,x+1,x+2,其中x∈N*,又设最小角为α,则
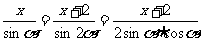 ,
,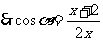 ①
①
又由余弦定理可得x2=(x+1)2+(x+2)2-2(x+1)(x+2)cosα
将①代入②整理得:x2-3x-4=0
解之得x1=4,x2=-1(舍)
所以此三角形三边长为4,5,6
评述: 此题所求为边长,故需利用正、余弦定理向边转化,从而建立关于边长的方程
例5已知三角形的一个角为60°,面积为10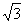 cm2,周长为20cm,求此三角形的各边长
cm2,周长为20cm,求此三角形的各边长
分析:此题所给的题设条件除一个角外,面积、周长都不是构成三角形的基本元素,但是都与三角形的边长有关系,故可以设出边长,利用所给条件建立方程,这样由于边长为三个未知数,所以需寻求三个方程,其一可利用余弦定理由三边表示已知60°角的余弦,其二可用面积公式S△ABC=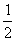 absinC表示面积,其三是周长条件应用
absinC表示面积,其三是周长条件应用
解:设三角形的三边长分别为a、b、c,B=60°,则依题意得
|

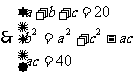
由①式得:b2=[20-(a+c)]2=400+a2+c2+2ac-40(a+c) ④
将②代入④得400+3ac-40(a+c)=0
再将③代入得a+c=13
由 ∴b1=7,b2=7
∴b1=7,b2=7
所以,此三角形三边长分别为5cm,7cm,8cm
评述: (1)在方程建立的过程中,应注意由余弦定理可以建立方程,也要注意含有正弦形式的面积公式的应用
(2)由条件得到的是一个三元二次方程组,要注意要求学生体会其求解的方法和思路,以提高自己的解方程及运算能力
正弦定理: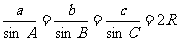
余弦定理: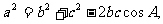

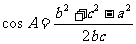


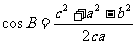
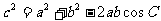 ,
,
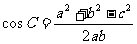
29.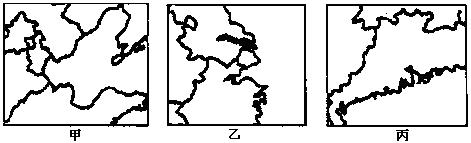 我国现有城市中约有1/2的城市缺水,严重缺水的城市约占1/6,每日缺水达1600万吨。下图所示三个地区均为我国沿海缺水城市集中分布地区。读图回答下列问题。
我国现有城市中约有1/2的城市缺水,严重缺水的城市约占1/6,每日缺水达1600万吨。下图所示三个地区均为我国沿海缺水城市集中分布地区。读图回答下列问题。
(1)针对甲图所示地区城市缺水状况,可采取的措施有大力开发地下水资源、跨流域调水和海水淡化等。其中目前比较可行的是_________,简述选择该措施的理由。
(2)乙图所示地区城市群位于我国东部湿润区和河流入海口,但仍有严重的缺水问题,试分析该地区城市缺水的人为原因。
(3)丙图所示地区经常出现“咸潮”,导致城市供水出现暂时性短缺。根据所掌握的地理知识,试分别从年份、季节、日期分析在哪些时候“咸潮”最为严重。
28.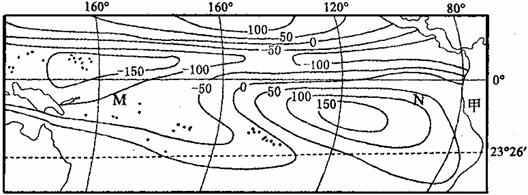 下图表示太平洋赤道附近海域多年平均蒸发量与降水量差值的分布。读图完成下列问题。
下图表示太平洋赤道附近海域多年平均蒸发量与降水量差值的分布。读图完成下列问题。
(1)比较M、N两海域的盐度大小,并分析原因。
(2)分析甲国沿海地区降水量异常增多对该国渔业生产的影响。
27.读图,回答下列问题。
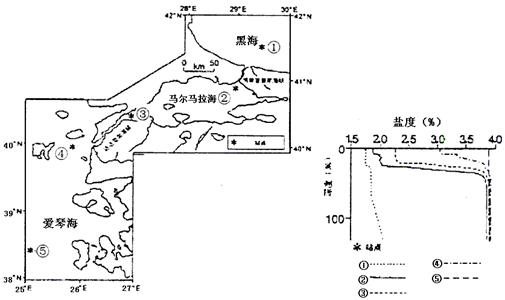
(1)土耳其海峡由图中的博斯普鲁斯海峡、马尔马拉海和达达尼尔海峡三部分组成。分析土耳其海峡地理位置的重要性。
(2)图中①②③④⑤5个站点中,表层海水盐度最低的是 ,分析该站点盐度低的原因。
(3)描述图中站点③海水盐度的垂直分布状况。
(4)1月份一艘轮船从黑海进入爱琴海,航行状况是 (顺、逆)水 (顺、逆)风。
26.下图为“水循环示意图”。读图回答下列问题。
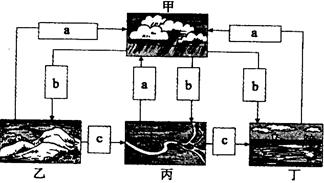
(1)图中丁→甲→丙→丁过程属于 循环。水循环的主要地理意义是 。
(2)水循环对乙图所示地区直接提供的资源主要有 和 资源。丙图中三角洲形成的主要外力作用是 。
(3)目前,人类直接利用的淡水资源主要来源于水循环的(填字母) 环节。人类可以通过 、 措施来改善水资源的时空分布,以更好地满足人类对水资源的需求。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com