
4、常用的对称关系
点(a,b)关于x轴的对称点(a,-b),关于y轴的对称点为(-a,b),关于原点的对称点(-a,-b)
关于直线y=x的对称点为(b,a),关于直线y=-x的对称点(-b,-a),关于直线y=x+m的对称点为(b-m,a+m),关于直线y=-x+m的对称点(m-b,m-a).
3.曲线关于点(中心),直线(轴)的对称问题的一般思想是用代入转移法。
(1)曲线f(x,y)=0关于点A(a,b)的对称曲线的方程是f(2a-x,2b-y)=0
(2)曲线f(x,y)=0关于直线Ax+By+c=0的对称曲线的求法:
设所求曲线上任一点P(x,y)关于直线Ax+By+c=0对称点P0(x0,y0),在已知曲线f(x,y)=0上,由两点关于直线对称的解法,求得x0,y0,代入f(x0,y0)=0,即得对称曲线方程。
2.点关于直线的对称点
即对称轴为两对称点连线的“垂直平分线“,利用”垂直“和”平分“这两个条件建立方程组,就可求出对称点的坐标,方法:
设点(x0,y0)关于直线Ax+By+c=0的对称点(x’,y’),则
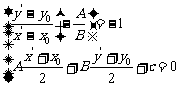
1.点(x,y)关于点(a,b)的对称点的坐标为(2a-x,2b-y)
事实上,点关于点的对称的对称中心恰恰是这两点为端点的线段的中点,因此中心对称的问题是线段中点坐标公式的应用问题。
2.掌握判断曲线(或曲线间)对称的方法.
1.掌握求已知曲线的轴对称曲线和中心对称曲线方程的方法.
18.菜学校的地理兴趣小组到我国东南沿海的一个小岛进行野外考察,设计完成了相关实验。现在邀请你和他们一起研究。
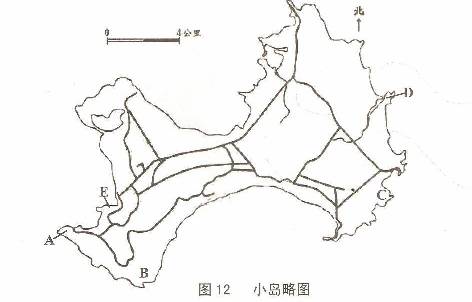
(1)兴趣小组到了海滨沙滩,实地勘察岩石并探究其成因。他们在不同地点拍摄了以下景观照片,大家谓之“鬼斧神T”。请你分析形成A、B两地岩石景观的主要地质作用。
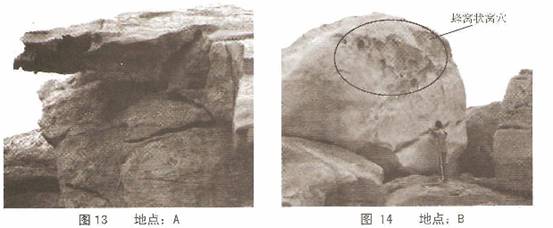
(2)在D地发现不同的岩石高度不一,图15中伟晶岩脉比围岩凸出2-11 cm;圈16中基性岩脉比花岗岩凹下5-90 cm。请你分析原因,并按分析结果排列图中的三种岩石(岩脉)。

 (3)在D地观测到不少岩层变动(见图17-图19):在图17中发现岩面局部呈褶曲斑蚀痕,图18和图19有不同岩脉的穿插。据此分析该地的地壳变动情况并按形成早晚排列图18和图19中的岩石(岩脉)。
(3)在D地观测到不少岩层变动(见图17-图19):在图17中发现岩面局部呈褶曲斑蚀痕,图18和图19有不同岩脉的穿插。据此分析该地的地壳变动情况并按形成早晚排列图18和图19中的岩石(岩脉)。

(4)在B地和D地,兴趣小组见到了沙丘(见图20)图9中的箭头是沙丘两翼的突出方向。同学们观测了风吹沙的连续过程(见图20-图23);为深入研究,兴趣小组实地测量了B地不同风速携带的沙量,见表2,还比较了不同位置沙的粒径,见表3。请分析:①图20中的箭头的指向;②要分析不同位置沙的粒径,还要对表3的数据进行怎样的处理?请把任意一行的处理结果填在表2对应的空格内;③分析表2和表3你得出什么结论?
表2:实地测量海滨不同风速携带沙量(单位g)
|
日期 |
时间 |
风速(m/s) |
沙粒位置 |
携带量(g) |
|
4.21 |
16:22 |
9 |
沙丘上 |
16.5 |
|
4.24 |
16:22 |
9 |
沙丘上 |
16.6 |
|
4.25 |
10:00 |
4.2 |
沙丘上 |
3.2 |
|
4.25 |
10:00 |
4.2 |
沙滩上 |
1.9 |
|
4.28 |
16:00 |
9.7 |
沙丘上 |
16.8 |
|
4.28 |
16:00 |
9.7 |
沙滩上 |
5.9 |
表3:不同位置沙粒粒径分析
|
采样点 |
>0.42mm |
0.297-0.21mm |
0.21-0.125mm |
<0.125mm |
||||
|
沙丘上 |
0g |
|
4.0g |
|
169.75g |
|
48.35g |
|
|
沙丘旁 |
7.8g |
|
58.45g |
|
126.75g |
|
31.4g |
|
|
沙滩上 |
180.3g |
|
13.4g |
|
79.6g |
|
9.4g |
|


5)在考察途中兴趣小组还了解到,一种我国南方地区普遍丰富的自然资源在岛上却
十分短缺。这种资源是什么?短缺的原冈是什么?请你为当地提出解决该问题的措施。
25.材料一 我国大学生毕业人数2007年为495万人,2008年为559万人,2009年为610万人,就业率仅为8%。而目前的国际金融危机,又使许多企业减少了新增的岗位。而大学生自主创业的比例从2007年的1.2%提升到2009年2%。
材料二 从2004年到2009年,党中央、国务院把就业放在经济社会发展的突出位置,实施积极的就业政策。党的十七大提出,实施扩大就业的发展战略,促进以创业带动就业。
(1) 从经济生活角度说明促进高校毕业生自主创业的重要意义.
(2)有人认为,政府实施积极的就业政策,就能解决劳动者就业问题。运用经济生活的相关地此观点进行分析。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com