6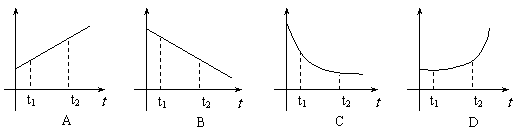．上海“明珠线”某轻轨车站的设计方案如图所示，与站台相连的轨道有一个小的坡度，设站台与水平轨道的高度差为h，列车的总质量为m，关于这个设计方案的优点，下列描述不确切的是

A．进站过程中，重力沿斜坡的分力是阻力，有利于制动

B．出站过程中，重力沿斜坡的分力是动力，有利于启动

C．进站过程中，有mgh的动能转化为重力势能

D．在一次进站、停靠、出站的整个过程中，节约的能量是2mgh

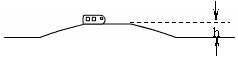
5．如图所示，Q是单匝金属线圈，MN是一个螺线管，它的绕线方法没有画出，Q的输出端a、b和MN的输入端c、d之间用导线相连，P是在MN的正下方水平放置的用细导线绕制的软弹簧线圈．若在Q所处的空间加上与环面垂直的变化磁场，发现在t₁至t₂时间段内弹簧线圈处在收缩状态，则所加磁场的磁感应强度的变化情况可能为

4．如图所示，置于水底A点的光源发出一细束复色光射向水面，经折射后分裂成三束，下列有关这三种光的性质的描述正确的是

A．1在水中传播的时间最短

B．3的光子能量最小

C．增大入射角i，1最先消失

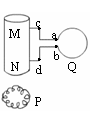D．从水中进入空气，三束光对应的单个光子能量均不变

3．为了解决农村电价居高不下的问题，有效地减轻农民负担，1999年至2000年，在我国广大农村普遍实施了“农网改造”工程，工程包括两项主要内容：(1)更新变电设备，提高输电电压；(2)更新电缆，减小输电线电阻．若某输电线路改造后输电电压变为原来的2倍，线路电阻变为原来的0.8倍，在输送的总功率不变的条件下，线路损耗功率将变为原来的

A．0.4倍　　　 B．0.32倍　　　　

C．0.2倍　　　 D．0.16倍

2．关于分子热运动和布朗运动,下列说法正确的是

A．固体微粒越大，同一时刻与之碰撞的液体分子越多，布朗运动越显著

B．布朗运动是分子无规则运动的反应

C．当物体的温度达到0℃时,物体分子的热运动就会停止

D．布朗运动的剧烈程度和温度有关，所以布朗运动也叫热运动

1．关于核能和核反应下列说法正确的是

A．根据E=mC²可知物体所具有的能量和它的质量之间存在着简单的正比关系

B．根据ΔE=ΔmC²，在核裂变过程中减少的质量转化成了能量

C．太阳内部进行的热核反应属于重核的裂变

D．当铀块的体积小于临界体积时就会发生链式反应，瞬时放出巨大能量

21．(本小题满分14分)

设f(x)=ax2+bx+c(a＞b＞c),f(1)=0,g(x)=ax+b.

(1)求证：函数y=f(x)与y=g(x)的图象有两个交点；

(2)设f(x)与g(x)的图象交点A、B在x轴上的射影为A1、B1，求｜A1B1｜的取值范围；

(3)求证：当x≤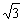－时，恒有f(x)＞g(x).

20．(本小题满分12分)

已知定点Q(6，0)和抛物线y2=8x上的两个动点A(x1，y1)、B(x2，y2)，其中A、B的横坐标x1、x2满足x1≠x2，且x1+x2=4．

(I)证明线段AB的垂直平分线过定点Q；

(Ⅱ)当A、B两点的距离为何值时，△AQB的面积最大？

19．(本小题满分12分)

某公司欲建连成片的网球场数座，用128万元购买土地10000平方米，该球场每座的建设面积为1000平方米，球场的总建筑面积的每平方米的平均建设费用与球场数有关，当该球场建x个时，每平方米的平均建设费用用f(x)表示，且f(n)=f(m)(1+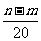)(其中n＞m,n∈N)，又知建五座球场时，每平方米的平均建设费用为400元，为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和)，公司应建几个球场?

(16)如图，为了解某海域海底构造，在海平面内一条直线上的A，B，C三点进行测量，已知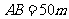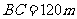，，于A处测得水深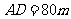，于B处测得水深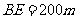，于C处测得水深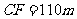，求∠DEF的余弦值。 　　　　

(17)如图，在三棱锥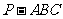中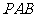，⊿是等边三角形，∠PAC=∠PBC=90 º

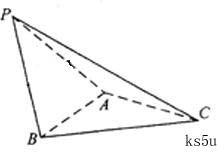(Ⅰ)证明：AB⊥PC

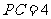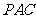(Ⅱ)若，且平面⊥平面，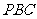　　　

求三棱锥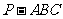体积。

18．(本小题满分12分)

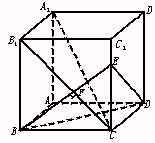已知长方体AC1中，棱AB＝BC＝3，棱BB1＝4，连结B1C，过B点作B1C的垂线交CC1于E，交B1C于F.

(1)求证A1C⊥平面EBD；

(2)求点A到平面A1B1C的距离；

(3)求平面A1B1C与平面BDE所成角的度数；

(4)求ED与平面A1B1C1所成角的大小；