8．若P为△ABC所在平面外一点，且PA⊥平面ABC，平面PAC⊥平面PBC，求证：BC⊥AC.

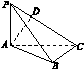
证明：∵平面PAC⊥平面PBC，作AD⊥PC垂足为D，

根据平面与平面垂直的性质定理知：AD⊥平面PBC，则BC⊥AD，

又PA⊥平面ABC，则BC⊥PA，∴BC⊥平面PAC.因此BC⊥AC.

7．已知P是△ABC所在平面α外一点，O是点P在平面α内的射影

(1)若P到△ABC的三个顶点的距离相等，则O是△ABC的__________；

(2)若PA、PB、PC与平面α所成的角相等，则O是△ABC的__________；

(3)若P到△ABC三边距离相等，且O在△ABC的内部，则O是△ABC的__________；

(4)若平面PAB、PBC、PCA与平面α所成的角相等，且O在△ABC的内部，则O是△ABC的__________；

(5)若PA、PB、PC两两垂直，则O是△ABC的________．

答案：(1)外心　(2)外心　(3)内心　(4)内心　(5)垂心

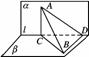
6．一条线段的两个端点分别在一个直二面角的两个面内，则这条线段与这两个平面所成的角的和的范围是________．

解析：作AC⊥l垂足为C，作BD⊥l垂足为D，连结BC、AD，

则∠BAD和∠ABC分别为直线AB和平面α和β所成角．

由cos∠ABD＝cos∠ABC·cos∠DBC≤cos∠ABC，

即∠ABD≥∠ABC，∠ABC+∠BAD≤∠ABD+∠BAD＝90°.

答案：(0°，90°]

5．α、β是两个不同的平面，m、n是平面α及β之外的两条不同的直线，给出四个论断：①m⊥n；②α⊥β；③n⊥β；④m⊥α，以其中三个论断作为条件，剩余的一个论断作为结论，写出你认为正确的一个命题____________．

答案：可填①③④⇒②与②③④⇒①中的一个

4．矩形ABCD中，AB＝4，BC＝3，沿AC将矩形ABCD折成一个直二面角B－AC－D，则四面体ABCD的外接球的体积为(　)

A.π　 　　　　　　 B.π　 　　　　　　　　 C.π　 　　　　　 D.π

答案： C

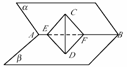
3．二面角α－AB－β的平面角是锐角，C∈α，CD⊥β，垂足为D，E∈AB，且∠CEB是锐角，则∠CEB与∠DEB的大小关系为(　)

A．∠CEB＞∠DEB　 　　　 B．∠CEB＜∠DEB

C．∠CEB≤∠DEB　 　　　 D．∠CEB与∠DEB的大小关系不确定

解析：如下图：作DF⊥AB垂足为F，连结CF由三垂线定理知∠CFD为二面角的平面角，可知∠CED，∠DEB均为锐角，cos∠CEB＝cos∠DEB·cos∠CED＜cos∠DEB，即∠CEB＞∠DEB.

答案： A

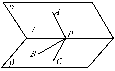
2．二面角α－l－β的大小为锐角，P∈l，PA⊂α，PB⊂β且PA⊥l，则(　)

A．∠APB的最大值等于二面角的平面角

B．∠APB的最小值等于二面角的平面角

C．二面角的平面角既不是∠APB的最大值，也不是∠APB的最小值

D．∠APB就是二面角的平面角

解析：如右图，在平面β内作PC⊥l，则∠APC为二面角的平面角，cos∠APB＝cos∠BPC·cos∠APC≤cos∠APC，即∠APB≥∠APC，故选B.

答案： B

1．设m、n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题，其中正确命题的序号是(　)

①若m⊥α，n∥α，则m⊥n；②若α∥β，β∥γ，m⊥α，则m⊥γ；③若m∥α，n∥α，则m∥n；④若α⊥γ，β⊥γ，则α∥β.

A．①和②　 B．②和③　 C．③和④　 D．①和④

答案：A

37．(8分)塑料购物袋是日常生活中的易耗品。它在为消费者提供便利的同时，由于过量使用及回收处理不到位等原因，造成了严重的能源资源浪费和环境污染。塑料购物袋问题引起了社会各界的广泛关注。到2007年底，全国有10多个省市地方政府，在本地人大代表和政协委员的建议和督促下，相继出台并实施了限制使用塑料购物袋的规定。在总结各地方实践经验的基础上，国务院发布了《关于限制生产销售使用塑料购物袋的通知》(简称“限塑令”)，并决定于2008年6月1日起在全国范围实施。国务院通知要求，采取禁止生产、销售、使用超薄塑料购物袋，实行塑料购物袋有偿使用制度等六项措施，以促进资源综合利用，保护生态环境。

运用矛盾主次方面的知识分析发布“限塑令” 的哲学依据。

临颍二高2009-2010学年度(下期)高二年级第一次月考

36.(14分)科学执政、民主执政、依法执政，是党执政能力建设的总目标，也是新形势下党个更好执政的根本要求和基本方略。为实现执政的科学化、民主化、法制化，我国在改革和完善党的领导方式和执政方式、改革和完善决策机制、深化行政管理体制改革、深化干部人事改革制度、加强对权力的制约和监督等五个方面，力推新执政理念。

(1)结合材料，运用所学哲学知识，说明为什么要力推新执政理念？(6分)

(2)运用辩证唯物主义认识论的有关道理，说明怎样才能力推新执政理念？(8分)