
1、已知集合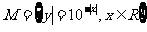
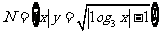 则
则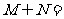 ( )
( )
A.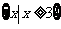 B.
B.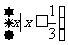 C.
C.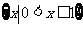 D.
D.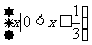
22、已知定义域为R的函数f (x)=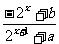 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f (t2-2t)+ f (2t2-k)<0恒成立,求k的取值范围.
21、在四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB为等边三角形.
(1)求PC与平面ABCD所成角的大小;
(2)求二面角B-AC-P的大小;
(3)求点A到平面PCD的距离.
20、(文)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约。乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是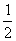 ,且面试是否合格互不影响。求:
,且面试是否合格互不影响。求:
(1)至少有1人面试合格的概率;
(2)没有人签约的概率。
(理)某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试,已知每个科目只允许有一次补考机会,两个科目成绩均合格可获得证书,现某人参加这项考试,科目A每次考试成绩合格的概率均为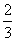 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为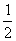 ,假设各次考试成绩合格与否均互不影响。
,假设各次考试成绩合格与否均互不影响。
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为ξ,求ξ的数学期望Eξ.
19、已知函数f(x)=3x,且f-1(18)=a+2,g(x)=3ax-4x的定义域区间为[-1,1].
(1)求g(x)的解析式;
(2)判断g(x)的单调性;
(3)若方程g(x)=m有解,求m的取值范围.
18、设函数f(x)=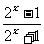
(1)求f(x)的反函数
(2)判断f-1(x)在其定义域内的单调性
17、已知集合A={x||x-2|<a,a>o},集合B={x|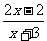 <1}
<1}
(1)若a=1,求A∩B
(2)若A⊊B,求实数a的取值范围
16、将函数f(x)=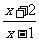 的图象向左平移一个单位,再向下平移一个单位后,得到函数g(x)的图象,则g(1)+2 g(2)+3 g(3) = .
的图象向左平移一个单位,再向下平移一个单位后,得到函数g(x)的图象,则g(1)+2 g(2)+3 g(3) = .
15、函数y=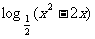 的单调递减区间是 .
的单调递减区间是 .
14、(文)定义在R上的函数f (x)满足f (x+1)=- f (x), 且f (x)=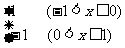 ,
,
则f (3)= .
(理)函数f (x) 对于任意实数x满足条件f (x+2)=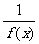 ,若f (1)=-5,
,若f (1)=-5,
则f [f (5)] = .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com