
6. 函数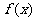 对任意正整数
对任意正整数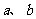 满足条件
满足条件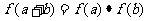 ,且
,且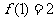 。则
。则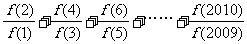 的值是( )
的值是( )
A.2009 B.2010 C.2008 D.2007
5. 函数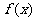 的定义域为
的定义域为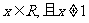 ,已知
,已知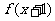 为奇函数,当
为奇函数,当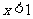 时,
时,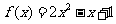 ,那么当
,那么当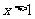 时,
时,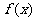 的解析式为( )
的解析式为( )
A.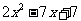 B.
B. C.
C.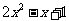 D.
D.
4. 若函数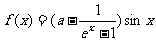 是偶函数,则常数
是偶函数,则常数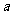 等于( )
等于( )
A.-1 B.1 C.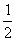 D.
D.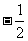
3. 已知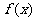 的定义域是
的定义域是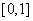 ,且
,且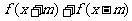 的定义域是
的定义域是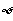 ,则正数
,则正数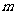 的取值范围是( )
的取值范围是( )
A.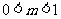 B.
B.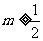 C.
C.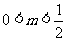 D.
D.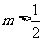
2. 如果命题“非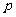 或非
或非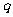 ”是假命题,则下列各结论正确的是( )
”是假命题,则下列各结论正确的是( )
①命题“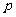 且
且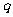 ”是真命题 ②命题“
”是真命题 ②命题“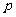 且
且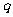 ”是假命题
”是假命题
③命题“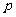 或
或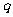 ”是真命题 ④命题“
”是真命题 ④命题“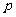 或
或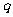 ”是假命题
”是假命题
A.②③ B.②④ C.①③ D.①④
1. 已知集合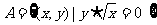 ,
,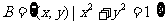 ,
,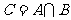 ,则
,则 中元素的个数是( )
中元素的个数是( )
A.1 B.2 C.3 D.4
22、解:(Ⅰ)当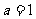 时,
时,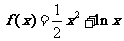 ,
,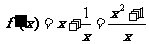 ;………2分
;………2分
对于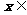 [1,e],有
[1,e],有 ,∴
,∴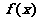 在区间[1,e]上为增函数,…3分
在区间[1,e]上为增函数,…3分
∴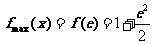 ,
,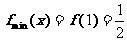 .……………………………5分
.……………………………5分
(Ⅱ)令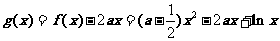 ,
,
则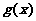 的定义域为(0,+∞).…………6分
的定义域为(0,+∞).…………6分
在区间(1,+∞)上函数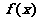 的图象恒在直线
的图象恒在直线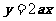 下方等价于
下方等价于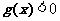 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立.
∵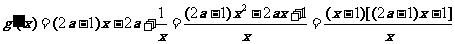
① 若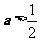 ,令
,令 ,得极值点
,得极值点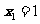 ,
,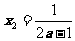 ,
,
当 ,即
,即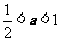 时,在(
时,在(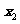 ,+∞)上有
,+∞)上有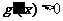 ,
,
此时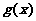 在区间(
在区间(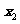 ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有
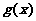 ∈(
∈(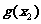 ,+∞),不合题意;………………………………………8分
,+∞),不合题意;………………………………………8分
当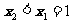 ,即
,即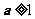 时,同理可知,
时,同理可知,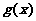 在区间(1,+∞)上,有
在区间(1,+∞)上,有
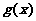 ∈(
∈(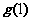 ,+∞),也不合题意;………………………………………9分
,+∞),也不合题意;………………………………………9分
② 若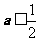 ,则有
,则有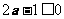 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有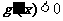 ,
,
从而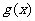 在区间(1,+∞)上是减函数;……………………………………10分
在区间(1,+∞)上是减函数;……………………………………10分
要使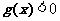 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
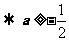 ,
,
由此求得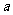 的范围是[
的范围是[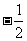 ,
,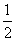 ].
].
综合①②可知,当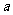 ∈[
∈[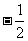 ,
,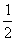 ]时,
]时,
函数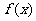 的图象恒在直线
的图象恒在直线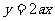 下方. ………………12分
下方. ………………12分
21、解:(Ⅰ)已知式即 ,故
,故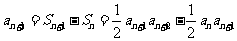 .
.
因为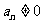 ,当然
,当然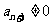 ,所以
,所以
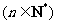 .
.
由于 ,且
,且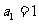 ,故
,故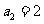 .
.
于是 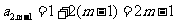 ,
,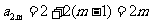 ,
,
所以 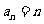
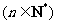 . ……………4分
. ……………4分
(Ⅱ)由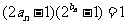 ,得
,得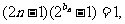
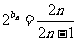 ,
,
故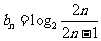 .从而
.从而 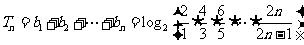 .
.
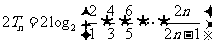
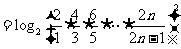
因此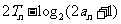
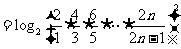
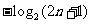
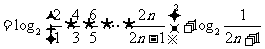
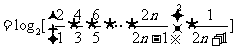 .
.
设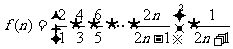 ,
,
则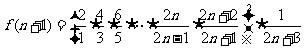 ,
,
故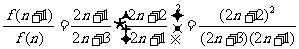
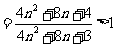 ,
,
注意到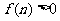 ,所以
,所以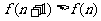 .
.
特别地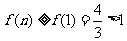 ,从而
,从而 .
.
所以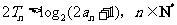 .
………………12分
.
………………12分
22.(本小题满分12分)已知函数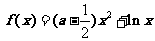 .(
.(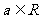 )
)
(Ⅰ)当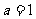 时,求
时,求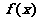 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数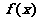 的图象恒在直线
的图象恒在直线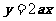 下方,求
下方,求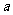 的取值范围.
的取值范围.
21、(本小题满分12分)
已知数列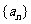 的前
的前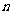 项和为
项和为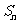 ,且
,且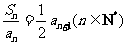 ,其中
,其中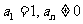 .
.
(Ⅰ)求数列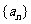 的通项公式;
的通项公式;
(Ⅱ)设数列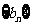 满足
满足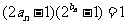 ,
,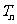 为
为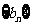 的前
的前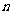 项和,求证:
项和,求证:
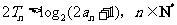 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com