
分数指数幂的意义,分数指数幂与根式的互化,有理指数幂的运算性质.
2.用分数指数幂表示下列各式:
(1)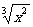 (2)
(2)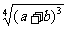 (a+b>0)
(a+b>0)
(3) (4)
(4) (m>n)
(m>n)
(5)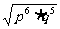 (p>0) (6)
(p>0) (6)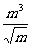
解:(1) 
(2) 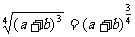
(3) 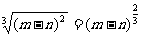
(4)  =(m-n)2
=(m-n)2
(5) 
(6) 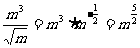
1.用根式的形式表示下列各式(a>0)
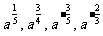
解: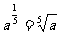
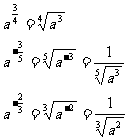
例1求值: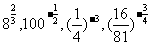 .
.
解:

例2用分数指数幂的形式表示下列各式:
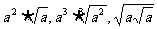 (式中a>0)
(式中a>0)
解: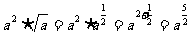
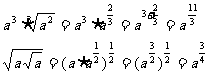
例3计算下列各式(式中字母都是正数)

分析:(1)题可以仿照单项式乘除法进行,首先是系数相乘除,然后是同底数幂相乘除,并且要注意符号
(2)题按积的乘方计算,而按幂的乘方计算,等熟练后可简化计算步骤
解
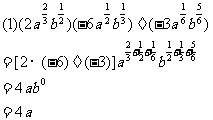
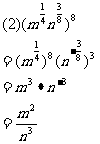
例4计算下列各式:

分析:(1)题把根式化成分数指数幂的形式,再计算
(2)题先把根式化成分数指数幂的最简形式,然后计算
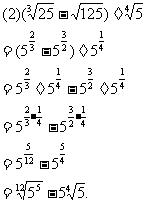
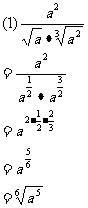 解:
解:
3.有理指数幂的运算性质:

说明:若a>0,P是一个无理数,则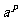 表示一个确定的实数,上述有理指数幂的运算性质,对于无理数指数幂都适用,有关概念和证明在本书从略.?
表示一个确定的实数,上述有理指数幂的运算性质,对于无理数指数幂都适用,有关概念和证明在本书从略.?
2.规定:
(1) (a>0,m,n∈N*,且n>1)
(a>0,m,n∈N*,且n>1)
(2)0的正分数指数幂等于0.
(3)0的负分数指数幂无意义.
规定了分数指数幂的意义以后,指数的概念就从整数推广到有理数指数.当a>0时,整数指数幂的运算性质,对于有理指数幂也同样适用.即对于任意有理数r,s,均有下面的运算性质.
1.正数的正分数指数幂的意义
 (a>0,m,n∈N*,且n>1)
(a>0,m,n∈N*,且n>1)
要注意两点:一是分数指数幂是根式的另一种表示形式;二是根式与分数指数幂可以进行互化.
另外,我们还要对正数的负分数指数幂和0的分数指数幂作如下规定.
3.引例:当a>0时
①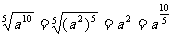
②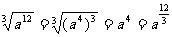
③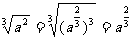
④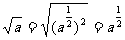
上述推导过程主要利用了根式的运算性质,例子③、④、⑤用到了推广的整数指数幂运算性质(2).因此,我们可以得出正分数指数幂的意义.
2.根式的运算性质:
①当n为任意正整数时,(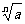 )
) =a.
=a.
②当n为奇数时, =a;当n为偶数时,
=a;当n为偶数时, =|a|=
=|a|= .
.
⑶根式的基本性质: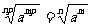 ,(a
,(a 0)
0)
用语言叙述上面三个公式:
⑴非负实数a的n次方根的n次幂是它本身.
⑵n为奇数时,实数a的n次幂的n次方根是a本身;n为偶数时,实数a的n次幂的n次方根是a的绝对值.
⑶若一个根式(算术根)的被开方数是一个非负实数的幂,那么这个根式的根指数和被开方数的指数都乘以或者除以同一个正整数,根式的值不变.
1.整数指数幂的运算性质:

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com