
3、已知直线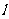 的方程为:
的方程为:
(1)求证:不论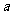 取何值,直线
取何值,直线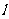 恒过定点;
恒过定点;
(2)记(1)中的定点为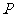 ,若
,若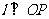 (
(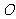 为原点),求实数
为原点),求实数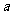 的值.
的值.
2、 已知直线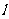 过点
过点 且与
且与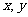 轴分别交于
轴分别交于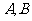 两点.
两点.
(1)若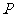 为
为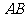 中点,求直线
中点,求直线 的方程;(2)若
的方程;(2)若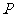 分
分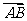 所成的比为
所成的比为 ,求
,求 的方程.
的方程.
练习11.1(3)
补充练习
1、(1)若直线过两点 ,则
,则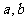 分别叫做该直线在
分别叫做该直线在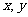 轴上的截距.当
轴上的截距.当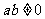 时,求直线
时,求直线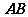 的方程;
的方程;
(2)若过点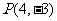 的直线
的直线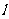 在两坐标轴上截距相等,求直线
在两坐标轴上截距相等,求直线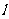 的方程.
的方程.
(二)一般式方程
1、概念引入
由直线的点方向式方程和点法向式方程,我们可以发现,平面直角坐标系中的每一条直线都可以用一个关于 的二元一次方程表示;那么每一个关于
的二元一次方程表示;那么每一个关于 的二元一次方程
的二元一次方程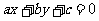 (
(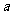 ,
,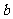 不同时为0)是否都表示一条直线呢?
不同时为0)是否都表示一条直线呢?
2、概念形成
直线的一般式方程的定义
直线的点方向式方程和直线的点法向式方程经过整理,成为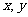 的二元一次方程
的二元一次方程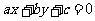 .
.
反之,任意二元一次方程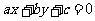
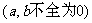 都是直线方程么?回答是肯定的.首先,当
都是直线方程么?回答是肯定的.首先,当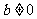 时,方程可化为
时,方程可化为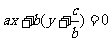 ,根据直线点法向式方程可知,这是过点
,根据直线点法向式方程可知,这是过点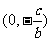 ,以
,以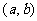 为一个法向量的直线;当
为一个法向量的直线;当 时,方程为
时,方程为 ,由于
,由于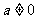 ,方程化为
,方程化为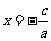 ,表示过点
,表示过点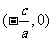 且垂直于
且垂直于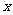 轴的直线.
轴的直线.
所以二元一次方程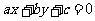
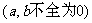 是直线的方程,叫做直线的一般式方程.
是直线的方程,叫做直线的一般式方程.
3、例题解析
例1 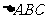 中,已知
中,已知 、
、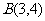 ,求
,求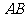 边的中垂线的一般式方程.
边的中垂线的一般式方程.
解 直线过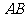 中点
中点 ,
,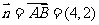 ,则其点法向式方程为
,则其点法向式方程为 ,整理为一般式方程
,整理为一般式方程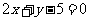 .
.
[说明]点法向式方程化为一般式方程.
例2(1)求过点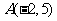 且平行于直线
且平行于直线 的直线方程;
的直线方程;
(2)求过点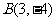 且垂直于直线
且垂直于直线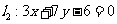 的直线方程.
的直线方程.
解 (1)解一: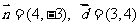 ,又直线过点
,又直线过点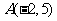 ,故直线的方程为
,故直线的方程为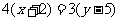 化简得
化简得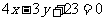 .
.
解二: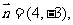 又直线过点
又直线过点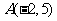 ,故直线的点法向式方程为
,故直线的点法向式方程为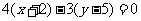 化简得
化简得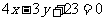 .
.
解三:设与 平行的直线方程为
平行的直线方程为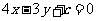 ,又直线过点
,又直线过点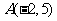 故
故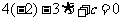 ,
,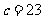 ,所以直线的方程是
,所以直线的方程是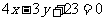 .
.
(2)解一: 的法向量
的法向量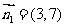 为所求直线的方向向量,又直线过点
为所求直线的方向向量,又直线过点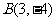 ,故直线的方程为
,故直线的方程为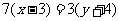 化简得
化简得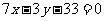 .
.
解二:设与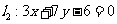 垂直的直线方程为
垂直的直线方程为 ,又直线过点
,又直线过点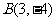 故
故 ,
, ,所以直线的方程是
,所以直线的方程是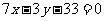 .
.
[说明]一般地,与直线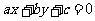 平行的直线可设为
平行的直线可设为 ;而与直线
;而与直线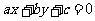 垂直的直线可设为
垂直的直线可设为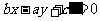 .
.
例3能否把直线方程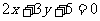 化为点方向式方程?点法向式方程?若能,它的点方向式方程和点法向式纺方程是否唯一?并观察x、y的系数与方向向量和法向量有什么联系?
化为点方向式方程?点法向式方程?若能,它的点方向式方程和点法向式纺方程是否唯一?并观察x、y的系数与方向向量和法向量有什么联系?
解: 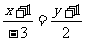 、
、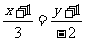 、
、 、
、 ……
……
 、4(x+4)+6(y-1)=0……
、4(x+4)+6(y-1)=0……
能够化成点方向式的形式,并且有无数个!
所有的方向向量之间存在:一个非零实数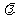 ,使得
,使得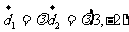 ;
;
易得点法向式方程也是不唯一的,并且有无数个!
所有的法向量之间存在:一个非零实数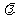 ,使得
,使得
变式:直线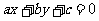 的方向向量可以表示为
的方向向量可以表示为
直线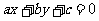 的法向量可以表示为
的法向量可以表示为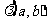
[说明]注意直线的一般式方程和点方向式方程与点法向式方程的联系.
(一)点法向式方程
1、概念引入
从上一堂课的教学中,我们知道,在平面上过一已知点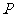 ,且与某一方向平行的直线
,且与某一方向平行的直线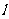 是惟一确定的.同样在平面上过一已知点
是惟一确定的.同样在平面上过一已知点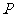 ,且与某一方向垂直的直线
,且与某一方向垂直的直线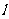 也是惟一确定的.
也是惟一确定的.
2、概念形成
直线的点法向式方程
在平面上过一已知点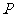 ,且与某一方向垂直的直线
,且与某一方向垂直的直线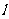 是惟一确定的.建立直角坐标平面,设
是惟一确定的.建立直角坐标平面,设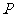 的坐标是
的坐标是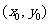 ,方向用非零向量
,方向用非零向量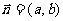 表示.
表示.
直线的点法向式方程的推导
设直线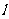 上任意一点
上任意一点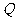 的坐标为
的坐标为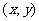 ,由直线垂直于非零向量
,由直线垂直于非零向量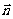 ,故
,故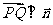 .根据
.根据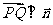 的充要条件知
的充要条件知 ,即:
,即: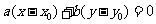 ①;反之,若
①;反之,若 为方程⑤的任意一解,即
为方程⑤的任意一解,即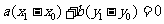 ,记
,记 为坐标的点为
为坐标的点为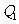 ,可知
,可知 ,即
,即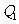 在直线
在直线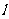 上.综上,根据直线方程的定义知,方程⑤是直线
上.综上,根据直线方程的定义知,方程⑤是直线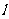 的方程,直线
的方程,直线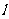 是方程①的直线.
是方程①的直线.
我们把方程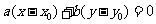 叫做直线
叫做直线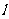 的点法向式方程,非零向量
的点法向式方程,非零向量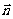 叫做直线
叫做直线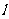 的法向量.
的法向量.
3、概念深化
从上面的推导看,法向量 是不唯一的,与直线垂直的非零向量都可以作为法向量.
是不唯一的,与直线垂直的非零向量都可以作为法向量.
若直线的一个方向向量是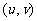 ,则它的一个法向量是
,则它的一个法向量是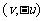 .
.
4、例题解析
例1 已知点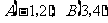 ,求
,求 的垂直平分线
的垂直平分线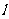 的点法向式方程.
的点法向式方程.
解 由中点公式,可以得到 的中点坐标为
的中点坐标为 ,
,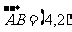 是直线
是直线 的法向量,
的法向量,
所以, 的垂直平分线
的垂直平分线 的点法向式方程.
的点法向式方程.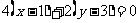
[说明]关键在于找点和法向量!
例2已知点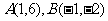 和点
和点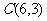 是三角形的三个顶点,求
是三角形的三个顶点,求
(1)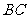 边所在直线方程;
边所在直线方程;
(2)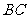 边上的高
边上的高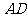 所在直线方程.
所在直线方程.
解(1)因为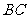 边所在直线的一个方向向量
边所在直线的一个方向向量 =(7,5),且该直线经过点
=(7,5),且该直线经过点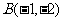 ,所以
,所以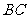 边所在直线的点方向式方程为
边所在直线的点方向式方程为
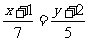
(2)因为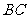 边上的高
边上的高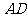 所在的直线的一个法向量为
所在的直线的一个法向量为 =(7,5),且该直线经过点
=(7,5),且该直线经过点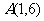 ,所以高
,所以高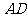 所在直线的点法向式方程为
所在直线的点法向式方程为
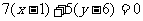

5、巩固练习
练习11.1(2)
直线的点法向式方程以及一般式方程;
在理解直线方程的意义,掌握直线的点方向式方程的基础上,进一步探究点法向式方程以及一般式方程;学会分类讨论、数形结合等数学思想,形成探究能力.
本节的重点是直线的点法向式方程以及一般式方程的推导及应用.在上一堂课的基础上,通过向量垂直的充要条件(对应坐标的关系式)推导出直线的点法向式方程.引导同学发现直线的点方向式方程、点法向式方程都可以整理成关于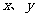 的一次方程
的一次方程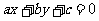 (
( 不全为零)的形式.
不全为零)的形式.
本节的难点是通过对直线与二元一次方程关系的分析,初步认识曲线与方程的关系并体会解析几何的基本思想!从而培养学生用坐标法对平面直线(和以后的圆锥曲线)的研究能力.
13.(1)CaCl2溶液和NaHCO3溶液反应生成CaCO3沉淀。为表示这个反应写出了下列两个反应方程式:
CaCl2 + NaHCO3 == CaCO3↓+ NaCl + HCl
CaCl2 + 2 NaHCO3 == CaCO3↓+ 2 NaCl + CO 2↑+ H2O
你认为哪一个反应的化学方程式不合理,并简述理由。
(2)已知难溶的物质在一定条件下可转化成更难溶的物质。将白色Mg(OH)2加到FeCl3溶液中有红棕色沉淀生成。请写出反应的化学方程式并简述理由。14.小海、小林、小明三同学一起测定双氧水溶液中溶质的质量分数。
查阅资料:2H2O22H2O+O2↑;常温下氧气密度为1.42g/L。
设计原理:将一定质量的双氧水样品与二氧化锰混合,测定反应产生的氧气的质量,计算出H2O2的质量,继而得双氧水溶液中溶质的质量分数。
过程方法:(1)小海首先设计(如左图):向装有样品溶液(20 g)的锥形瓶(75 g)中投入0.5g二氧化锰,待双氧水反应完毕后测得锥形瓶和反应后混合物的总质量为95.1 g,则产生氧气的质量是 g,双氧水溶液中溶质的质量分数为 。
 (2)小林对小海的设计提出质疑后,设计如中图的方案(只在上述方案中的锥形瓶上加一干燥管),请你说明小林质疑的理由是
。
(2)小林对小海的设计提出质疑后,设计如中图的方案(只在上述方案中的锥形瓶上加一干燥管),请你说明小林质疑的理由是
。
(3)小明通过思考后,觉得他们的方案误差都较大,于是小明设计如右图的方案(试剂用量不变)。请你说明小明认为他们误差较大的原因:
。如果要满足小明的要求,该实验需用 mL的量筒。
12.研究性学习小组选择从空气中制取氮气作为研究课题,以下是他们设计的实验方案:
 |
|||
|
|||
(1)除去二氧化碳和水蒸气:右图A装置中发生反应的化学方程式是________,
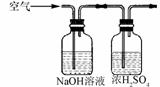 B装置中浓硫酸的作用是_______________。
B装置中浓硫酸的作用是_______________。

 (2)除去氧气:他们分别收集一瓶气体用右下图装置进行除去氧气的燃烧实验,其中甲同学选用红磷,乙同学选用木炭。你认为:选用____________ (填“红磷”或“木炭”)的方法不科学,
(2)除去氧气:他们分别收集一瓶气体用右下图装置进行除去氧气的燃烧实验,其中甲同学选用红磷,乙同学选用木炭。你认为:选用____________ (填“红磷”或“木炭”)的方法不科学,
原因是__________________________________________。
 (3)分析误差:此法得到的氮气密度(标准状况下)经科学测定,与氮气的实际密度有误差,请你分析出现误差的可能原因(只写两种,不考虑计算误差):①_____________________ ;② __________________。
(3)分析误差:此法得到的氮气密度(标准状况下)经科学测定,与氮气的实际密度有误差,请你分析出现误差的可能原因(只写两种,不考虑计算误差):①_____________________ ;② __________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com