
1.知识与技能
体验零点存在性定理的形成过程,理解零点存在性定理,并能应用它探究零点的个数及存在的区间.
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
||||||||||||||||||||||||
|
复习引入 |
观察下列三组方程与函数
利用函数图象探究方程的根与函数图象与x轴的交点之间的关系 |
师生合作 师:方程x2 – 2x –3 = 0的根为–1,3函数y = x2 – 2x – 3与x轴交于点(–1,0) (3,0)  生:x2 – 2x + 1 = 0有相等根为1.  函数y= x2 – 2x + 1与x轴有唯一交点 (1,0).  x2 – 2x + 3 = 0没有实根  函数y = x2 – 2x + 3与x轴无交点 |
以旧引新,导入课题 |
||||||||||||||||||||||||
|
概念形成 |
1.零点的概念 对于函数y=f (x),称使 y=f (x)= 0的实数x为函数 y=f (x)的零点  2.函数的零点与方程根的关系  方程f (x) = 0有实数根 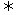 函数 函数 y = f (x)的图象与x轴有交点 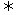 函数y = f (x)的零点 函数y = f (x)的零点 3.二次函数零点的判定  对于二次函数y = ax2 + bx + c与二次方程ax2 + bx + c,其判别式△= b2 – 4ac 
|
师:我们通俗地称函数与x轴交点的横坐标为函数的零点,请同学归纳零点的定义 师:考察函数①y = lgx  ②y = lg2(x + 1) ③y = 2x  ④y = 2x – 2的零点  生:①y = lgx的零点是x = 1  ②y = lg2(x + 1)的零点是x=0  ③y = 2x没有零点  ④y = 2x – 2的零点是x = 1 |
归纳总结 感知概念  分析特征  形成概念 |
||||||||||||||||||||||||
|
概念深化 |
引导学生回答下列问题 ①如何求函数的零点?  ②零点与图象的关系怎样? |
师生合作,学生口答,老师点评,阐述 生①零点即函数为零对应的自变量的值,零点即对应方程的根  ②零点即函数图象与x轴交点的横坐标  ③求零点可转化为求方程的根 |
以问题讨论代替老师的讲援 |
||||||||||||||||||||||||
|
应用举例 |
练习1.求函数y = –x2 – 2x
+ 3的零点,并指出y>0,y = 0的x的取值范围 练习2.求函数y =x3 – 2x2 – x + 2的零点,并画出它的图象 练习3.利用函数图象判断下列方程有没有根,有几个根:(1) –x2+3x+5 = 0;(2)2x (x–2) = –3; (3)x2 = 4x – 4; (4)5x2+2x=3x2+5. |
学生自主尝试练习完成练习1、2、3 生:练习1解析:零点–3,1 x∈(–3,1)时y>0  时y<0 时y<0练习2解析:因为x3–2x2–x+2 = x2 (x – 2) – (x – 2) = (x–2) (x2–1) = (x – 2) (x – 1) (x + 1), 所以已知函数的零点为–1,1,2. 3个零点把x轴分成4个区间:  ,[–1,1],[1,2], ,[–1,1],[1,2],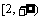 在这4个区间内,取x的一些值(包括零点),列出这个函数的对应值表:
在直角坐标系内描点连线,这个函数的图象如图所示
练习3解析:(1)令f (x) = –x2 + 3x + 5,作出函数f (x)的图象,它与x轴有两个交点,所以方程–x2 + 3x + 5 = 0有两个不相等的实数根. (2)2x (x – 2) = –3可化为2x2–4x+3=0 令f (x) = 2x2–4x+3作出函数f (x)的图象,它与x轴没有交点,所以方程2x (x – 2) = –3无实数根 (3)x2 = 4x – 4可化为x2 – 4x + 4 = 0,令f (x) = x2 – 4x + 4,作出函数f (x)的图象,它与x轴只有一个交点(相切),所以方程x2 = 4x – 4有两个相等的实数根 (4)5x2+2x=3x2+5可化为2x2 + 2x – 5 = 0,令f (x) = 2x2 + 2x–5,作出函数f (x)的图象,它与x轴有两个交点,所以方程5x2+2x=3x2+5有两个不相等的实数根
师:点评板述练习的解答过程 |
让学生动手练习或借助多媒体演示,加深对概念的说明,培养思维能力 |
||||||||||||||||||||||||
|
归纳总结 |
(1)知识方面 零点的概念、求法、判定 (2)数学思想方面 函数与方程的相互转化,即转化思想 借助图象探寻规律,即数形结合思想 |
学生归纳,老师补充、点评、完善 |
回顾、反思、归纳知识,提高自我整合知识的能力 |
||||||||||||||||||||||||
|
课后作业 |
3.1 第一课时 习案 |
学生独立完成 |
固化知识,提升能力 |
备选例题
例:已知a∈R讨论关于x的方程|x2 – 6x + 8| = a的实数解的个数.
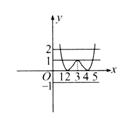 [解析]令f (x) = |x2 – 6x + 8|,g (x) = a,在同一坐标系中画出f (x)与g (x)的图象,如图所示,
[解析]令f (x) = |x2 – 6x + 8|,g (x) = a,在同一坐标系中画出f (x)与g (x)的图象,如图所示,
f (x) = | (x – 3)2 – 1|,
下面对a进行分类讨论,由图象得,
当a<0时,原方程无实数解;
当a = 0时,原方程实数解的个数为3;
当0<a<1时,原方程实数解的个数为4;
当a>1或a = 0时,原方程实数解的个数为2.
在相对熟悉的问题情境中,通过学生自主探究,合作交流中完成的学习任务.尝试指导与自主学习相结合.
重点:理解函数零点的概念,掌握函数零点与方程根的求法.
难点:数形结合思想,转化化归思想的培养与应用.
3.情感、态度与价值观
在体验零点概念形成过程中,体会事物间相互转化的辨证思想,享受数学问题研究的乐趣.
2.过程与方法
由一元二次方程的根与一元二次函数的图象与x轴的交点情况分析,导入零点的概念,引入方程的根与函数零点的关系,从而培养学生的转化化归思想和探究问题的能力.
1.知识与技能
(1)理解函数零点的意义,了解函数零点与方程根的关系.
(2)由方程的根与函数的零点的探究,培养转化化归思想和数形结合思想.
15. (18分)如图甲,将一质量为0.4kg的足够长的绝缘均匀细管置于光滑水平地面上,管的内表面粗糙。有一质量为0.1kg,带电量为0.1C的带正电小球沿细管轴线方向以一定速度向右进入管内,细管内径略大于球的直径,空间存在如如图所示的匀强磁场,磁感应强度
(18分)如图甲,将一质量为0.4kg的足够长的绝缘均匀细管置于光滑水平地面上,管的内表面粗糙。有一质量为0.1kg,带电量为0.1C的带正电小球沿细管轴线方向以一定速度向右进入管内,细管内径略大于球的直径,空间存在如如图所示的匀强磁场,磁感应强度
B=1T(g=10m/s2)。
(1)当细管固定时,在图乙中画出小球在管中运动的初速度v0和最终稳定速度vt的关系。(取水平向右为正方向)
(2)若细管不固定,带电小球以20m/s的初速度进入管内,且整个运动过程中细管没有离开地面,则系统最终产生的内能为多少?
13.(16分) 如图所示,给静止在光滑水平面上的质量为8kg的小车施加一水平向右的恒力F。当小车的速度达到1.5m/s时,在小车右端相对地面无初速地放上一个质量为2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小车足够长,设最大静摩擦力与滑动摩擦力相同,求:
(1) 若F=8N,从物块放上小车开始计时,经t=1.5s物块对地的位移大小;
(2) 若F=25N,从物块放上小车开始计时,经t=1.5s物块对地的位移大小。(g取10m/s2)

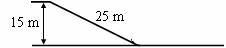
14(18分)倾斜雪道的长为25 m,顶端高为15 m,下端经过一小段圆弧过渡后与很长的水平雪道相接,如图所示。一滑雪运动员在倾斜雪道的顶端以水平速度v0=8 m/s飞出,在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起。除缓冲外运动员可视为质点,过渡轨道光滑,其长度可忽略。设滑雪板与雪道的动摩擦因数μ=0.2,求运动员在水平雪道上滑行的距离(取g=10 m/s2)
12.在测定电阻的实验中,比较简便、直观的方法有半偏法、替代法等:
①.在测定电流表内阻Rg的实验中,使用如图甲所示的电路,当S2断开,S1闭合,且R1调到9900Ω时,电流表的指针转到满偏0.2mA,再闭合S2,将R2调到90Ω时,电流表指针恰好指在一半刻度,则电流表的内阻Rg= Ω,此值较Rg的真实值
(填偏大、偏小或相等).
② 在用替代法测电阻的实验中,测量电路如乙图所示,图中R是滑动变阻器,Rs是电阻箱,Rx是待测高阻值电阻,S2是单刀双置开关,G是电流表。
(1).按电路原理图将丙图(图中已连好4根导线)所示的器材连成测量电路。
(2).实验按以下步骤进行,并将正确答案填在图中横线上。
A.将滑动片P调至电路图中滑动变阻器的最右端,将电阻R调至最大,闭和开关S1,将开关S2拨向位置“1”,调节P的位置,使电流表指示某一合适的刻度I。
 B.再将开关S2拨向位置“2”,保持
位置不变,调节 ,使电流表指示的刻度仍为I。
B.再将开关S2拨向位置“2”,保持
位置不变,调节 ,使电流表指示的刻度仍为I。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com