
3.一物体做匀加速直线运动,若已知物体在第3s内的位移为s1和第7s内的位移为s2,则可求出物体的( )
①加速度 ②t=7.5s时的速度 ③在t=0~t=3s内的位移 ④物体发生10m的位移所需时间
A.① B.①② C.①②③ D.①④
2.物体从静止开始做匀加速直线运动,测得它在第n s内的位移为s,则物体运动的加速度为( )
A. B. C. D.
1.下列所描述的运动中,可能存在的是( )
A.速度变化很大,加速度很小 B.速度变化方向为正,加速度方向为负
C.速度变化越来越快,加速度越来越小 D.速度越来越大,加速度越来越小
4.(★★★★★)在一定温度下,把2.0体积N2和6.0体积H2通入一个带活塞的体积可变的容器中,活塞的一端与大气相通,如图20-2所示。容器中发生的反应如下:
N2+3H2 2NH3(正反应放热)
图20-2
2NH3(正反应放热)
图20-2
若反应达到平衡后,测得混合气体为7.0体积。试回答:
 (1)保持上述反应温度不变,设a、b、c(a∶b=1∶3)分别代表初始加入的N2、H2和NH3的体积,如果反应达到平衡后,混合气体中各物质的体积分数仍与上述平衡完全相同。那么:
(1)保持上述反应温度不变,设a、b、c(a∶b=1∶3)分别代表初始加入的N2、H2和NH3的体积,如果反应达到平衡后,混合气体中各物质的体积分数仍与上述平衡完全相同。那么:
①若a=1.0,c=2.0,则b=___________。在此情况下,反应起始时将向___________方向进行(填“正”或“逆)。
②若规定起始时反应向逆方向进行,则c的范围是__________________。(用含a、b的式子表示)。
(2)在上述装置中,若需控制平衡后混合气体为6.5体积,则可采取的措施是__________,原因是___________________________________。
3.(★★★★)在一个固定体积的密闭容器中,保持一定温度,进行以下反应:
H2(g)+Br2(g)  2HBr(g)
2HBr(g)
已知加入1 mol H2和2 mol Br2时,达到平衡后生成a mol HBr(见下表的“已知”项),在相同条件下,且保持平衡时各组分的含量不变,对下列编号(1)-(3)的状态,填写表中的空白。
|
编号 |
起始状态(mol) |
平衡时HBr(g) 物质的量(mol) |
||
|
H2 |
Br2 |
HBr |
||
|
已知 |
1 |
2 |
0 |
a |
|
(1) |
2 |
4 |
0 |
|
|
(2) |
|
|
1 |
0.5 a |
|
(3) |
m |
n(n≥2m) |
|
|
2.(★★★★)在一固定容积的密闭容器中,充入2.0 mol A和1.0 mol B发生如下反应:
2A(g)+B(g)  xC(g)
xC(g)
达到平衡后,C的体积分数为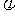 (C)。若维持容器体积和温度不变,改为充入0.6 mol A、0.3 mol B和1.4
mol C为起始物质,反应达平衡后,C的体积分数也为
(C)。若维持容器体积和温度不变,改为充入0.6 mol A、0.3 mol B和1.4
mol C为起始物质,反应达平衡后,C的体积分数也为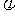 (C),则x可能为( )
(C),则x可能为( )
A.1 B.2 C.3 D.4
1.(★★★)将2.0 mol SO2气体和2.0 mol SO3气体混合于固定体积的密闭容器中,在一定条件下发生反应:2SO2(g)+O2(g)  2SO3(g),达到平衡时SO3为n mol。在相同温度下,分别按下列配比在相同密闭容器中放入起始物质,平衡时SO3等于n mol的是( )
2SO3(g),达到平衡时SO3为n mol。在相同温度下,分别按下列配比在相同密闭容器中放入起始物质,平衡时SO3等于n mol的是( )
A.1.6 mol SO2+0.3 mol O2+0.4 mol SO3
B.4.0 mol SO2+1.0 mol O2
C.2.0 mol SO2+1.0 mol O2+2.0 mol SO3
D.3.0 mol SO2+1.0 mol O2+1.0 mol SO3
2.恒温恒压条件下的等效平衡
恒温恒压条件下,建立等效平衡的条件是:相同反应物的投料比相等。若投料物质不相同时,可依反应方程式完全转化后作比较。如3 L带活塞的甲、乙两容器,保持 t℃和1标准大气压,甲中投入2 mol N2和5 mol H2,乙中投入4 mol N2和10 mol H2,建立平衡时,两容器中NH3体积分数相等。
●歼灭难点训练
1.恒温恒容条件下的等效平衡
恒温恒容条件下,建立等效平衡的条件是:反应物投料量相当。如在t℃的V L恒温恒容甲、乙两容器中,甲中投入2 mol SO2和1 mol O2,乙中投入2mol SO3,平衡时两容器中SO3的体积分数相等。
若某平衡反应为:
mA(g)+nB(g)  pC(g)+qD(g)
pC(g)+qD(g)
 且m+n=p+q,则压强对平衡无影响,这时建立等效平衡的条件是:相同反应物的投料比相等;若投料物质不一样时,可依反应方程式转化后再作比较。如温度t℃、体积为V L的甲、乙两恒温恒容容器中,甲中充入1 mol的I2蒸气和1 mol的H2,乙中充入3 mol的I2蒸气和3 mol的H2,那么平衡时,甲、乙两容器中HI的体积分数相同。
且m+n=p+q,则压强对平衡无影响,这时建立等效平衡的条件是:相同反应物的投料比相等;若投料物质不一样时,可依反应方程式转化后再作比较。如温度t℃、体积为V L的甲、乙两恒温恒容容器中,甲中充入1 mol的I2蒸气和1 mol的H2,乙中充入3 mol的I2蒸气和3 mol的H2,那么平衡时,甲、乙两容器中HI的体积分数相同。
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|||||||||||||||||||||||||||
|
提出问题引入课题 |
1问题:一元二次方程可用判别式判定根的存在性,可用求根公式求方程的根.但对于一般的方程,虽然可用零点存在性定理判定根的存在性,而没有公式. 求根:如何求得方程的根呢? ①函数f (x) = lnx + 2x – 6在区间(2,3)内有零点.  ②如果能够将零点所在的范围尽量缩小,那么在一定精确度的要求下,我们可以得到零点的近似值.  ③通过“取中点”的方法逐步缩小零点所在的范围.  ④取区间(2,3)的中点2.5,用计算器算得f (2.5)≈–0.084.因为f (2.5)·f (3)<0,所以零点在区间(2.5,3)内.再取内间(2.5,3)的中点2.75,用计算器算得f (2.75)≈0.512.因为f (2.5)·f (2.75)<0,所以零点在区间(2.5,2.75)内.  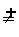 ⑤由于(2,3) (2.5,3) ⑤由于(2,3) (2.5,3) 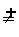 (2.5,2.75),所以零点所在的范围确实越来越小了. (2.5,2.75),所以零点所在的范围确实越来越小了. ⑥例如,当精确度为0.01时,由于|2.539 062 5 – 2.531 25| = 0.007 812 5<0.01,所以,我们可以将x = 2.531 25作为函数  f (x) = lnx + 2x – 6零点的近似值,也即方程lnx + 2x – 6 = 0根的近似值.  |
师:怎样求方程lnx + 2x – 6 = 0的根. 引导:观察图形  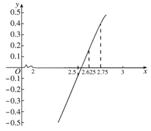  生:方程的根在(2,3)区间内  师:能否用缩小区间的方法逼近方程的根  生:应该可用  师:我们现用一种常见的数学方法-二分法,共同探究已知方程的根.  师生合作,借助计算机探求方程根的近似值. 
|
由旧到新设疑、析疑导入课题,实例分析了解二分法、进一步师生合作尝试二分法. |
|||||||||||||||||||||||||||
|
形成概念 |
1.对于区间[a,b]上连续不断且f (a)·f (b)<0的函数y = f (x),通过不断地把函数f (x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法. 2.给定精确度  ,用二分法求函数f (x)零点近似值的步聚如下: ,用二分法求函数f (x)零点近似值的步聚如下: (1)确定区间[a,b],验证f (a)·f (b)<0,给定精确度  ; ; (2)求区间(a,b)的中点c;  (3)计算f (c);  ①若f (c) = 0,则c就是函数的零点;  ②若f (a)·f (c)<0,则令b = c(此时零点x0∈(a,c));  ③若f (c)·f (b)<0,则令a = c(此时零点x0∈(c,b)).  (4)判断是否达到精确度  :即若|a – b|< :即若|a – b|< ,则得到零点近似值a(或b);否则重复2~4. ,则得到零点近似值a(或b);否则重复2~4. |
师生合作回顾实例: 求方程lnx + 2x – 6 = 0的近似解(精确度0.01)的操作过程.掌握二分法,总结应用二分法的步骤  师:讲授二分法的定义.  生:总结应用二分法的步骤.  学生交流总结,学生代表口述步骤,老师完善并板书. |
由特殊到一般形成概念,归纳总结应用二分法的步骤. |
|||||||||||||||||||||||||||
|
应用举例 |
 例1 借助计算器或计算机用二分法求方程2x + 3x = 7的近似解(精确度0.1). |
师生合作应用二分法,遵循二分法的步骤求解,并借助函数图象检验. 例1 解:原方程即2x + 3x –7 = 0,令f (x) = 2x + 3x –7,用计算器或计算机作出函数f (x) = 2x + 3x –7的对应值表与图象 
观察图或表可知f(1)·f(2)<0,说明这个函数在区间(1,2)内有零点x0. 取区间(1,2)的中点x1=1.5,用计算器算得f(1.5)≈0.33.因为f(1)·f(1.5)<0,所以x0∈(1,1.5). 再取(1,1.5)的中点x2=1.25,用计算器算得f(1.25)≈–0.87.因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5). 同理可得x0∈(1.375,1.5),x0∈(1.375,1.4375) 由于|1.375–1.4375| = 0.0625<0.1,所以,原方程的近似解可取为1.4375. |
尝试体验二分法,培养应用二分法从而固化基本理论技能 |
|||||||||||||||||||||||||||
|
巩固练习 |
1.借助计算器或计算机,用二分法求函数f(x) = x3 + 1.1x2 + 0.9x– 1.4在区间(0,1)内的零点(精确度0.1). 2.借助计算器或计算机,用二分法求方程x = 3 – lgx在区间(2,3)内的近似解(精确度0.1). |
学生动手尝试练习,师生借助计算机合作完成求解. 1.解:由题设可知f(0)= –1.4<0,f(1)=1.6>0, 于是f(0)·f(1)<0, 所以,函数f(x)在区间(0,1)内有一个零点. 下面用二分法求函数f(x) = x3 + 1.1x2 + 0.9x– 1.4在区间(0,1)内的零点 取区间(0,1)的中点x1=0.5,用计算器可算得f(0.5)= –0.55.因为f(0.5)·f(1)<0, 所以x0∈(0.5,1). 再取区间(0.5,1)的中点x2=0.75,用计算器可算得f(0.75)≈0.32. 因为f(0.5)·f(0.75)<0, 所以x0∈(0.5,0.75). 同理可得x0∈(0.625,0.75),x0∈(0.625,0.6875),x0∈(0.65625,0.6875) 由于|0.6875–0.65625|=0.3125<0.1, 所以原方程的近似解可取为0.65625. 2.解原方程即x + lgx– 3 = 0,令f(x) = x + lgx– 3,用计算器可算得f(2)≈–0.70,f(3)≈0.48, 于是f(2)· f(3)<0, 所以,这个方程在区间(2,3)内有一个解. 下面用二分法求方程x = 3 – lgx在区间(2,3)内的近似解. 取区间(2,3)的中点x1 = 2.5,用计算器可算得f(2.5)≈–0.10. 因为f(2.5)·f(3)<0,所以x0∈(2.5,3). 再取区间(2.5,3)的中点x2 = 2.75,用计算器可算得f(2.75)≈0.19.因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75). 同理可得x0∈(2.5,2.625), x0∈(2.5625,2.625). 由于|2.625–2.5625|=0.0625<0.1, 所以原方程的近似解可取为2.5625. |
进一步体验二分法,巩固应用二分法的方法与技巧及注意事项. |
|||||||||||||||||||||||||||
|
课后练习 |
3.1
第三课时 习案 |
学生独立完成 |
巩固二分法应用技能 |
备选例题
例1 用二分法求函数f (x) = x3 – 3的一个正实数零点(精确到0.1).
[解析]由于f (1) = –2<0,f (2) = 5>0,因此可以确定区间[1,2]作为计算的初始区间,用二分法逐步计算,列表如下:
|
端点或中点的横坐标 |
计算端点或中点的函数值 |
定区间 |
|
a0 = 1,b0 = 2 |
f(1)=
–2,f(2)=5 |
[1,2] |
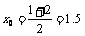 |
f (x0) = 0.375>0 |
[1,1.5] |
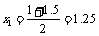 |
f (x1) = –1.0469<0 |
[1.25,1.5] |
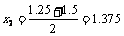 |
f (x2) = –0.4004<0 |
[1.375,1.5] |
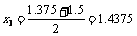 |
f (x3) = –0.0295<0 |
[1.4375,1.5] |
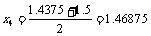 |
f (x4) = 0.1684>0 |
[1.4375,1.46875] |
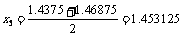 |
f (x5)>0 |
[1.4375,1.453125] |
|
x6 = 1.4453125 |
f (x6)>0 |
[1.4375,1.4453125] |
由上表的计算可知区间[1.4375,1.4453125]的左、右端点精确到0.1所取的近似值都是1.4,所以1.4可作为所求函数的一个正实数零点的近似值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com