
4. 已知 ,
,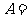
 ,
,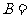
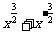 ,则
,则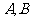 的值分别为( )
的值分别为( )
A. ,
, B.
B. ,
,
C.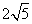 ,
,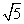 D.
D.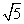 ,
,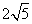
[填空题]
3.若函数y=ax+b-1(a>0且a≠1)的图象经过二、三、四象限,则一定有 ( )
A.0<a<1且b>0 B.a>1且b>0
C.0<a<1且b<0 D.a>1且b<0
2. ( 2005全国卷III)设 ,则
( )
,则
( )
(A)-2<x<-1 (B)-3<x<-2 (C)-1<x<0 (D)0<x<1
1.若 N*,则
N*,则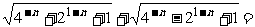 ( )
( )
A.2 B.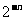 C.
C.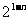 D.
D.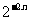
4.对于含有字母参数的指数式,必须对字母参数或自变量取值进行分类讨论,用好用活指数函数单调性,还要注意换元的灵活运用。
同步练习 2.9 指数 指数函数
[选择题]
3.指数函数y=ax(a>0,a≠1)的图象和性质,要分a>1与0<a<1来研究.
2.指数函数的定义重在“形式”,像y=2·3x,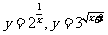 ,y=3x+1等都不是指数函数,是复合函数.
,y=3x+1等都不是指数函数,是复合函数.
1.根式的运算--根据分数指数幂的意义,转化为分数指数幂的运算;
[例1]已知9x-10·3x+9≤0,求函数y=(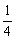 )x-1-4(
)x-1-4( )x+2的最大值和最小值.
)x+2的最大值和最小值.
解:由9x-10·3x+9≤0得(3x-1)(3x-9)≤0,解得1≤3x≤9.∴0≤x≤2.令( )x=t,则
)x=t,则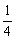 ≤t≤1,y=4t2-4t+2=4(t-
≤t≤1,y=4t2-4t+2=4(t- )2+1.当t=
)2+1.当t= 即x=1时,ymin=1;当t=1即x=0时,ymax=2.
即x=1时,ymin=1;当t=1即x=0时,ymax=2.
方法提炼 1.由不等式求x的范围;2.换元法转化为地次函数的闭区间上的最值问题..
[例2]已知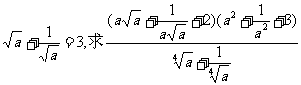 的值.
的值.
解: ,
,
 ,
,
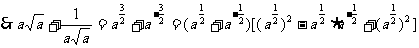
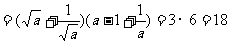 ,
,
而 ,
,

方法归纳 1.用好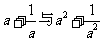 的关系.2.根式化分数指数幂再计算.
的关系.2.根式化分数指数幂再计算.
[例3](2004全国Ⅲ)解方程4x+|1-2x|=11.
解:当x≤0时,1-2x≥0.
原方程 4x-2x-10=0
4x-2x-10=0 2x=
2x= ±
±
 2x=
2x= -
- <0(无解)或2x=
<0(无解)或2x= +
+ >1知x>0(无解).
>1知x>0(无解).
当x>0时,1-2x<0.
原方程 4x+2x-12=0
4x+2x-12=0 2x=-
2x=- ±
±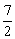
 2x=-4(无解)或2x=3
2x=-4(无解)或2x=3 x=log23(为原方程的解).
x=log23(为原方程的解).
思想方法 1.分类讨论--分段去绝对值;2。换元法。
[例4]设函数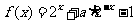 (a为实数).
(a为实数).
⑴若a<0,用函数单调性定义证明: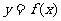 在
在 上是增函数;
上是增函数;
⑵若a=0,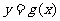 的图象与
的图象与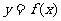 的图象关于直线y=x对称,求函数
的图象关于直线y=x对称,求函数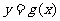 的解析式.
的解析式.
解: (1)设任意实数x1<x2,则f(x1)- f(x2)=
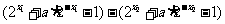
= =
=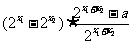

 .
.
又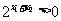 ,∴f(x1)- f(x2)<0,所以f(x)是增函数.
,∴f(x1)- f(x2)<0,所以f(x)是增函数.
(2)当a=0时,y=f(x)=2x-1,∴2x=y+1, ∴x=log2(y+1),
y=g(x)= log2(x+1).
[研究.欣赏](2002上海)已知函数
(1)证明f(x)在(-1,+∞)上为增函数;
(2)用反证法证明方程f(x)=0没有负数根。
证明(1)设-1<x1<x2

∵x2-x1>0,又a>1, ∴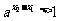 ,而-1<x1<x2,
,而-1<x1<x2,
∴x1+1>0, x2+1>0, ∴f(x2)-f(x1)>0,f(x)在(-1,+∞)上为增函数。
(2)设x0为方程f(x)=0的负根,则有 即
即
显然,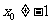 ,
,
若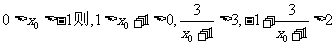
与 矛盾;
矛盾;
若x0<-1则,x0+1<0,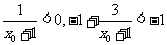 ,而
,而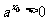 矛盾,即不存在x0<-1的解,综上知,不存在负根。
矛盾,即不存在x0<-1的解,综上知,不存在负根。
提炼方法: 1.方法:单调性定义,反证法,分类讨论;
2.反证法推矛盾时,体现了明确的目的性和数式变换的技巧和能力.
6.只须看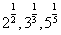 的大小,把
的大小,把 6次乘方, 把
6次乘方, 把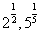 10次乘方可知c<a<b
10次乘方可知c<a<b
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com