
1.各类“地理计算”的关键知识与思路:
|
|
关键知识 |
计算思路 |
|
比例尺的计算 |
比例尺=图上距离/实地距离(在比例尺中,实际距离要将千米或米换算成厘米。求实际距离则要把得出的厘米换算成千米或米)。 |
1.先求出该图要表示的实际距离 2.算出图上要表示的距离 3.根据比例尺公式进行计算 |
|
地面高度、深度和温度的计算 |
①地面高度表示的两种方法: A 海拔:指地面某点高出海平面的垂直距离 B 相对高度:指地面某点高出另一地点的垂直距离 ②不同高度温度的差异:对流层中平均每上升100米,气温降低0·6℃。 ③地热增温率:在常温层以下,平均每加深100米,地温上升3℃(15千米以下,地热增温率逐渐减少;常温层深度,中纬比赤道和两极深,我国北方约为30米)。 |
|
|
地方时与经度的计算 |
掌握时间与经度的关系。即要掌握地球自转一周需要24小时,1小时转过15°经度,4分钟转过1°经度。 |
1.计算经度差 2.将经度差化为地方时差 3.某地地方时=已知地方时±4分钟/1°×两地经度差(所求地方时的地点,若在已知地的东面,则加时差;反之则减时差)。 |
|
时区和区时的计算 |
除中时区的中央经线是0°外,其余时区的中央经线都是15的倍数;相邻一个时区,区时相差1小时;东西12区的钟点相同,日期相差一天,自东十二区进入西十二区,日期要减去一天;自西十二区进入东十二区,日期要加上一天。此外,跨年月的计算要注意月大月小,平年和闰年二月份的天数;还要注意有无动程时间等要求。 |
1.先确定时区,求时区差 2.再按公式运算或图示法计算区时 ①时区的计算:某地时区序数=该地经度÷所得商数,再按数学求近似值的方法保留整数,小数点后4舍5入,就是该地的时区数。除中时区外,东经度为东时区,西经度为西时区。②区时的计算:某地的区时=已知地区时±1小时×两地时区差 两地时区差:若两地在中时区同侧,则时区数相减,两地在中时区的两侧,则时区数相加。若所求区时的地点在已知地的东边,则加时区差;若在已知地的西边则减时区差。 |
|
正午太阳高度角的计算 |
理解纬度变化和正午太阳高度角变化的关系,即纬度相差多少度,正午太阳高度角就相差多少度,即H=90°-纬度差 |
1.计算纬度差 2.利用图示法或计算公式运算正午太阳高度角 |
|
昼夜长短的计算 |
1.据日出日落时间,求昼夜长短计算公式:某地昼长=(正午12点-日出时间)×2;某地夜长=(子夜24点-日落时间)×2 2.在光照图上,昼夜长短的计算 读懂日照图,看出太阳此时直射哪一条经线,则此经线上各点为12点。 |
1.找出图上受太阳光直射的经线(确定为12点)2.算出某点所在纬线圈上的昼弧和夜弧所跨的经度范围3.根据经度和时间的关系,推算所求点的昼夜长短。 |
|
太阳日和恒星日的换算 |
理解太阳日与恒星日在自转周期上的差异 太阳日……360°59′……24小时 恒星日……360°……23时56分4秒 一个太阳日比一个恒星日多转了59′,的经度,时间上一个太阳日比恒星日多3分56秒。 |
|
|
地球运动线速度的计算 |
自转的线速度在赤道处最快,1670千米/小时,在南北纬60°处约为赤道的一半;公转线速度经过远日点时(7月初)速度较慢,在近日点时(1月初)速度较快,故从春分--秋分,约为186天,从秋分--春分约为179天。 |
|
|
经纬度距离的计算 |
掌握纬度每间隔1°之间的经线长度都相等,约为111千米。经度间隔1°之间的纬线长度长短不等,由赤道上的111千米向两极递减至零。 |
3.其他计算
|
计算类别 |
相关原理 |
|
气温计算 |
对流层气温垂直递减率:每上升100m,气温下降0.6℃ |
|
气压梯度的计算 |
单位距离的气压差 |
|
人口密度的计算 |
人口密度=人口总量/面积 |
|
人口自然增长率的计算 |
自然增长率=出生率-死亡率 |
|
城市化水平的计算 |
城市化水平等于城市人口数除以该地区总人口数 |
[要点深化与能力提升]
2.与地球运动有关的计算
|
计算类别 |
相关原理 |
|
地球自转线速度的计算 |
Vα=1670cosαkm/h。 |
|
恒星日及太阳日的相关计算 |
1太阳日比1恒星日长3分56秒。 |
|
时区、区时和地方时的计算 |
①某地时区序数=该地经度÷15º,对商四舍五入取整数;②东早西晚,经度每隔15º,地方时相差1小时;③各时区中央经线的地方时即为本时区的区时。 |
|
中心对称点的分布 |
地球上某点A(X,Y)关于球心的对称点坐标(X′,Y′),X′=1800-X(与X相反的经度),Y′与Y的数值相等,处于相反的半球。 |
|
不同日期的分界线及范围的计算 |
零时经线以东至日界线为地球上的“今天”, 以西至日界线为地球上的“昨天”。如果将地球分成“今天”和“昨天”,那么,“今天”所占地球的比重为(180°经线的地方时/24) |
|
太阳高度及正午太阳高度的计算 |
①太阳高度由太阳直射点(90º)向四周依次递减;昼半球>0º,夜半球<0º,晨昏线上为0º;②正午太阳高度的分布是由太阳直射点所在纬度向南北两侧递减,则H=90º-▲φ。 |
|
昼夜长短的计算 |
某地昼长等于该地所在纬线圈昼弧度数除以15º。日出时刻=12-昼长÷2;日落时刻=12+昼长÷2。 |
|
回归周期的计算 |
太阳直射点的回归运动(以北半球为例)周期为1回归年,即365日5时48分46秒。哈雷彗星的回归周期为76年。 |
|
太阳直射点坐标的计算 |
太阳直射点的特征:①正午太阳高度为90º的纬线;②地方时为12时的经线。 |
①时区、区时和地方时的计算
Ⅰ地方时:不同经度的时间。掌握东加西减、东早西晚的原则,每相差15度,时间上相差1小时,4分钟相差1度。根据已知时间求经度时,注意用时间的早晚来确定经度的东西方位。
Ⅱ区时:各地没有特殊说明情况下使用的时间。先掌握时区的计算,区时的计算方法与地方时的原则相同,每相差一个时区时间相差一个小时。注意地方时与区时的相互转换。
Ⅲ标准时:各国统一使用的时间。绝大部分国家只有一个标准时,多采用这个国家东部时区的区时,也有采用半区时的国家,如印度等;少数大国有两个标准时,如中国、美国、俄罗斯等。注意一个国家的任何地区,所使用的时间都为标准时,除非有特别说明是所在时区的区时或所在经线的地方时时例外。
Ⅳ北京时间:我国全国统一使用的时间,即东八区的区时,东经120度的地方时。注意北京时间不等于北京地方时,在有关日出日落时间的题目中多采用的是地方时。
⑵不同日期的分界线及范围的计算
①日期的变换有两种变换,即自然变换和人为变换。
自然变换是某地区时间为24点时,其日期事实上已是新的一天。
人为变换是指日界线,过日界线日期变换的原则是向东减一天,向西加一天。东、西十二区这两个半时区,在区时上是相同的,但日期上相差一天,东十二区是全球时间最早的地方,而西十二区是全球时间最晚的地方,即全球最东和最西的地方。
②全球总是被两条经线分割为两个日期,分割日期的经线分别是日界线和地方时为0时的经线,这两条经线可以重合,当二者重合的一瞬间,全球只有一个日期。注意真实的情况下,日界线和180度经线并非完全重合,在俄罗斯、阿留申群岛、南太平洋等地有明显弯曲。
今天范围的计算,采用的多为地方时。180度时间如果为T,那么地球上新的一天范围为T/124,旧的一天范围为(24-T)/24。也可以把T转化为北京时间Q,即Q=T-4。
如果使用的区时,那么新的一天范围可用时区数表示,时区数为180度经线的区时T+0.5个时区。注意一般情况下没有24点,它可表示第二天的0点。
⑶正午太阳高度的计算
①正午太阳高度的计算公式是:H=[90°-β(当地纬度和太阳直射点纬度)],其中β的求采用同一半球相减、不同半球相加的原则,永远取正值。
②利用垂直物体的日影计算:cotH=影长/物体长度。
③太阳能热水器的采光面与楼房顶面的夹角=β(β同①)
④南北半球中纬度地区楼房间隔L的计算:L=楼高×cotH°( H°即当地全年最小的正午太阳高度角,北半球为冬至日的正午太阳高度,南半球为夏至日的正午太阳高度)。在楼房布局时建议采用东北-西南向或西北-东南向。
⑤一个地区年正午太阳高度最大差值:
赤道地区是23°26’
南北半球热带地区介于23°26’和46°52′之间,具体度数是(当地纬度+23°26′)。
南北半球温带地区是46°52′。
南北半球寒带地区是46°52′,但也可以当作当地最大正午太阳高度的数值。
⑷昼夜长短的计算
①可以利用一个地区昼弧所跨的经度范围来计算,方法是在日照图上某条纬度与晨昏线有两上交点,两点之间在昼半球的部分即是白昼的时间。
②可以利用已知的日出和日落时间来求算。方法是:白昼长=2×(12-日出时间)或白昼长=2×(日落时间-12)。
③同一半球相同纬度地区昼长相同。而南北半球相同纬度地区的昼夜长短相反,如北纬40度的昼长是15时,那么南纬40度的地区夜长为15时。
④注意极昼区、极夜区的昼长分别是24时和0时。赤道地区的昼长永远是12时。
1.地图的计算
|
计算类别 |
相关原理 |
|
比例尺的计算 |
比例尺=图上距离/实地距离。 |
|
地理坐标(经纬度)的计算 |
①1º经线长为111km, 1º纬线长为111cosαkm(其中α为纬度);②北极星的地平高度等于当地纬度 |
|
海拔(绝对高度)和相对高度的计算 |
等高线图上任意两地相对高度的计算可根据: (n-1)d ≤▲H<(n+1)d(其中n表示两地间不同等高线的条数,d表示等高距。) |
⑴两地之间距离的计算
两地之间距离的计算主要有两种类型:一是已知比例尺求实际距离,只要量出所求两点之间的图上距离再用公式(实际距离=图上距离/比例尺)进行计算即可,需要注意的是单位一定要一致。二是通过经度或纬度差来进行计算,纬度差1度的经线长约为111千米,经度差1度的纬线长约等于111千米×cosφ(φ为所求地的纬度)。
⑵相对(断崖)高度的计算
断崖在等高线地形图上表现为若干条等高线的重叠处,其顶部的海拔高度应为几条重叠等高线中海拔最大值或之上,而底部的海拔高度应为几条重叠等高线中海拔最小值或之下,同时通过归纳得出,断崖的顶部和底部的相对高度H为:d(n-1)≤ H < d(n+1) (其中d为等高距,n为重叠的等高线条数)
10.设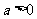 ,
,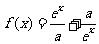 是
是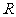 上的偶函数
上的偶函数
(1)求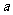 的值;(2)证明
的值;(2)证明 在
在 上为增函数
上为增函数
解:(1)依题意,对一切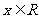 ,有
,有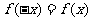 ,即
,即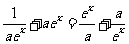
∴
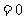 对一切
对一切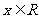 成立,则
成立,则 ,
,
∴ ,∵
,∵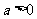 ,∴
,∴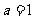
(2)(定义法)设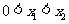 ,则
,则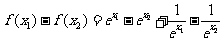
 ,
,
由 ,得
,得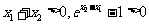 ,
,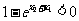 ,
,
∴ ,
,
即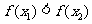 ,∴
,∴ 在
在 上为增函数
上为增函数
(导数法)∵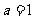 ,
,
∴
∴ 在
在 上为增函数
上为增函数
[探索题]定义在R上的奇函数f(x)满足f(x+2)=f(-x),当x∈(0,1]时,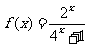 ;
;
(1)求证:f(x)是以4为周期的周期函数;
(2)求f(x)在[-1,0]上的解析式;
(3)若x∈[a,a+4],(a∈R),求使关于x的方程f(x)=λ有解的λ的取值范围.
解(1)∵f(x+4)=f[(x+2)+2]=f(-x-2)=-f(x+2)=f(x)
∴f(x)的周期为4.
(2)显然f(0)=0,当x∈[-1,0)时-x∈(0,1].
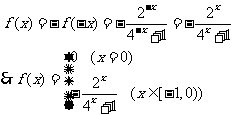
(3)

∴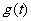 在(1,2]上是减函数,
在(1,2]上是减函数,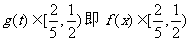
由 是奇函数,
是奇函数, 

又f(x+2)=f(-x),∴x=1是f(x)的对称轴.
 ,
, 
当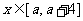 时,
时,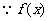 的周期为4,
的周期为4,
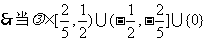 时,在[a,a+4]上可使方程
时,在[a,a+4]上可使方程 有解.
有解.
9.设f(x)= -2x+1,已知f(m)=
-2x+1,已知f(m)=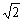 ,求f(-m).
,求f(-m).
解:设g(x)=
 -2x, 则
-2x, 则
g(-x)=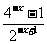 +2x=
+2x=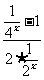 +2x
+2x
= +2x=
+2x= +2x=-
+2x=-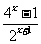 + 2x=-g(x)
+ 2x=-g(x)
g(x)是奇函数,g(m)= 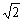 -1,
-1,
∴f(-m)=g(-m)+1=-g(m)+1=2-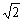 .
.
8.函数y=a2x+2ax-1(a>0,a≠1)在区间[-1,1]上的最大值为14,求a的值。
解:设t=ax,则y=t2+2t-1,在t≥-1时递增.而x∈[-1,1].
若a>1,则a-1≤t≤a, ymax=a2+2a-1=14, 解得a=3, (-5舍)
若0<a<1,则 a≤t≤a-1, ymin=a-2+2a-1-1=14, 解得
7. (1)求值

(2)若 ,求
,求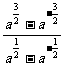 的值
的值
解(1)  =
=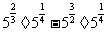

(2)原式=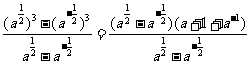

6.求值: =________
=________
简答提示: 1-4.AACD; 5. (-∞,1];6. 1;
[解答题]
5.函数y=( )
) 的递增区间是___________.
的递增区间是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com