
1.[江苏省赣榆高级中学2009年高考双周模拟试卷 ] (7分)
江苏宝胜集团是一家以生产电缆类产品为主的国家大型企业。在电缆生产过程中,不可避免地会产生一定量的含铜废料(如:零碎电缆)。某化学兴趣小组的四位同学得知这一情况后,围绕“从含铜废料中回收铜”提出了各自的看法。
甲同学根据已学知识,提出了一套回收方案:

 乙同学在查阅资料后得知:在通入空气并加热的条件下,铜可与稀硫酸在溶液中发生
乙同学在查阅资料后得知:在通入空气并加热的条件下,铜可与稀硫酸在溶液中发生
反应(方程式为:2Cu + 2H2SO4 + O2 2CuSO4 + 2H2O),于是他提出了另一套方案:

(1)从环保角度对两套方案的不同部分进行比较,你认为 (填“甲”或“乙”)的方案更合理。理由是: 。
(2)丙认为,无论是甲还是乙的方案,在“加铁屑”这一步时,应该加入略过量的铁屑。你认为丙这么说的道理是: 。丁又提出了疑问:“如果铁过量,剩余的铁会混在红色粉末中,该怎么处理呢?”。请提出你的想法:
。
(3)最后,老师肯定了同学们的积极思考,但同时指出:方案最后一步所得浅绿色滤液结晶后,会得到一种俗称“绿矾”的工业产品,可增加经济效益。请写出使“绿矾”结晶的两种可能方法: 、 (“绿矾”溶解度随温度升高而增大)。如果直接排放掉滤液,不仅造成了浪费,还会 。
答案.(1)乙 。甲方案第一步“灼烧”会产生污染空气的气体、粉尘、烟雾。(关键词:“污染空气”)
(2)“确保CuSO4 用完”或“将Cu完全置换出来”,其他类似说法均可。
将所得铜粉酸洗后再洗涤、干燥;或过滤前在加适量的酸以除去剩余的铁粉。
(3)蒸发 、降温 。 水污染或环境污染。
19.(理) 解 (1)∵x2-2x+2恒正, ∴f(x)的定义域是1+2ax>0,
即当a=0时,f(x)定义域是全体实数。
当a>0时,f(x)的定义域是(-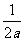 ,+∞)
,+∞)
当a<0时,f(x)的定义域是(-∞,-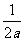 )…………5分
)…………5分
(2)当b>1时,在f(x)的定义域内,f(x)>0
 >1
>1 x2-2x+2>1+2ax
x2-2x+2>1+2ax
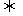 x2-2(1+a)x+1>0
其判别式Δ=4(1+a)2-4=4a(a+2)
x2-2(1+a)x+1>0
其判别式Δ=4(1+a)2-4=4a(a+2)
(i)当Δ<0时,即-2<a<0时 ∵x2-2(1+a)x+1>0
∴f(x)>0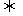 x<-
x<-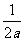 …………10分
…………10分
(ii)当Δ=0时,即a=-2或0时
若a=0,f(x)>0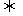 (x-1)2>0
(x-1)2>0 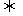 x∈R且x≠1
x∈R且x≠1
若a=-2,f(x)>0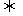 (x+1)2>0
(x+1)2>0 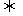 x<
x<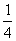 且x≠-1…………15分
且x≠-1…………15分
(iii)当△>0时,即a>0或a<-2时
方程x2-2(1+a)x+1=0的两根为 x1=1+a-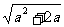 ,x2=1+a+
,x2=1+a+
若a>0,则x2>x1>0>-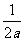
∴ 或
或
若a<-2,则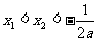
∴f(x)>0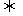 x<1+a-
x<1+a- 或1+a+
或1+a+ <x<-
<x<-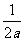
综上所述:当-2<a<0时,x的取值集合为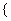 x|x<-
x|x<-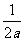
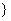
当a=0时,x∈R且x≠1,x∈R,当a=-2时: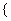 x|x<-1或-1<x<
x|x<-1或-1<x<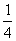
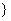
当a>0时,x∈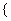 x|x>1+a+
x|x>1+a+ 或-
或-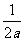 <x<1+a-
<x<1+a-
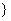
当a<-2时,x∈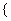 x|x<1+a-
x|x<1+a- 或1+a+
或1+a+ <x<-
<x<-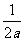
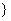 ………20分
………20分
(文)解:(Ⅰ)根据题意: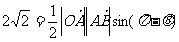
即 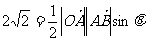 ,---------4分
,---------4分
又 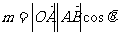
以上两式相除,并整理得: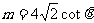 -----------8分
-----------8分
∵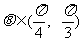 ,∴
,∴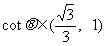 ∴实数
∴实数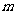 的取值范围是
的取值范围是 . 10分
. 10分
(Ⅱ)解一:由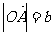 知点
知点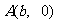 ,设点
,设点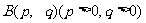 ,则
,则
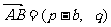 ,
,
于是 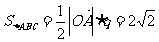 ,
,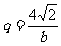 ,------12分
,------12分
又 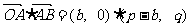
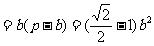
∴ 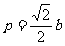 ,
-----------16分
,
-----------16分
从而 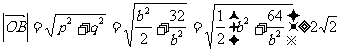 ,当且仅当
,当且仅当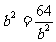 即
即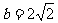 时,取等号, 此时,点
时,取等号, 此时,点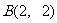 ,代入
,代入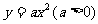 解得
解得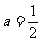 ,
,
∴ 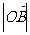 取得最小值
取得最小值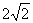 时,
时,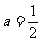 . ------20分
. ------20分
(Ⅱ)解二:∵ 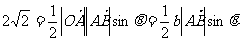 ,
,
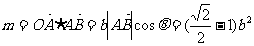 ,-------12分
,-------12分
∴ 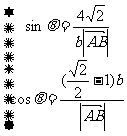 ∴
∴ 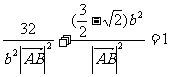 ,
,
即 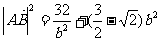 ,-------14分
,-------14分
∴ 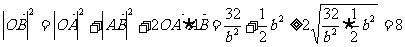 ,
,
当且仅当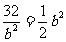 即
即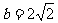 时,取等号,---------16分
时,取等号,---------16分
此时,点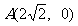 , 由
, 由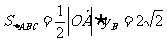 求得点
求得点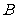 纵坐标
纵坐标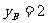 ,
,
代入 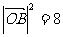 求得点
求得点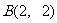 , 代入
, 代入 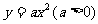 解得
解得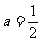 ,
,
∴ 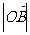 取得最小值
取得最小值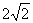 时,
时,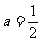 .-------20分
.-------20分
18. 解:由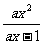 >x得
>x得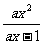 -x>0即
-x>0即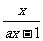 >0(2分)
>0(2分)
此不等式与x(ax-1)>0同解.(3分)
 x>0
x<0
x>0
x<0
①若a<0,则 或
ax-1>0 ax-1<0
得: 或
或
即 无解 或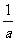 <x<0. ∴解集为(
<x<0. ∴解集为(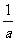 ,0).(4分)
,0).(4分)
②若a=0,则-x>0 x<0,∴解集为(-∞,0).(6分)
x<0,∴解集为(-∞,0).(6分)
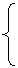
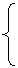 x>0 x<0
x>0 x<0
③若a>0,则 或
ax-1>0 ax-1<0
得 或
或
即:x>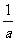 或x<0,∴解集为(-∞,0)∪(
或x<0,∴解集为(-∞,0)∪(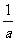 ,+∞)(9分)
,+∞)(9分)
综上所述:①当a<0时,不等式的解集是(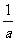 ,0)
,0)
②当a=0时,不等式的解集是(-∞,0)
③当a>0时,不等式的解集是(-∞,0)∪(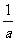 ,+∞)(10分)
,+∞)(10分)
17. 解:(I)由题意及正弦定理,得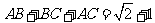 ,
,
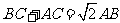 ,
两式相减,得
,
两式相减,得 .
.
(II)由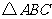 的面积
的面积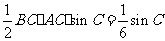 ,得
,得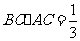 ,
,
由余弦定理,得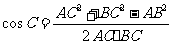
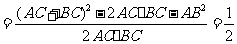 ,
,
所以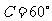 .
.
16. 解:(1)设 ,有
,有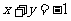 ①
①
由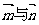 夹角为
夹角为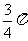 ,有
,有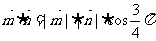 .
.
∴ ②
由①②解得
②
由①②解得
∴即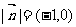 或
或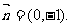
(2)由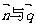 垂直知
垂直知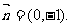
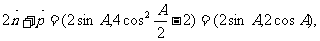
∴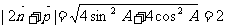
15. 解:设 L: y-4=k(x-1) , (k<0) L在两轴上的截距分别为a,b.
则a=1-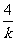 , b=4-k , 因为 k<0, -k>0,
, b=4-k , 因为 k<0, -k>0, 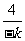 >0
>0
a+b=5+(-k)+ 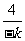
 5+2
5+2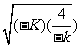 =5+4=9 。
=5+4=9 。
当且仅当 -k=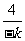 即 k= -2 时
a+b 取得最小值9。
即 k= -2 时
a+b 取得最小值9。
所以,所求的直线方程为y-4=-2(x-1) , 即 2x+y-6=0
1、D 2,A 3,C 4,A 5,A 6,B 7, D 8,D 9, C 10,D
二,填空题
11, -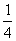 12, (3,1) 13,
12, (3,1) 13, 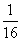 14,
14,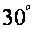
三,解答题
19.设函数f(x)=logb (b>0且b≠1),
(b>0且b≠1),
(1)求f(x)的定义域;
(2)当b>1时,求使f(x)>0的所有x的值。
甘肃省天水市一中2008-2009学年度高一第二学期期末
数 学 试 题
18.(本小题12分)解关于x的不等式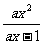 >x,(a∈R).
>x,(a∈R).
17.(本题10分)已知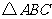 的周长为
的周长为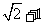 ,且
,且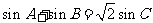 .
.
(I)求边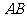 的长;
的长;
(II)若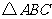 的面积为
的面积为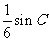 ,求角
,求角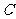 的度数.
的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com