2、作出的角可能是异面直线所成的角，也可能是它的邻补角，在直观图中无法判定，只有通过解三角形后，根据这个角的余弦的正、负值来判定这个角是锐角(也就是异面直线所成的角)或钝角(异面直线所成的角的邻补角)。最后作答时，这个角的余弦值必须为正。

51. 已知空间四边形ABCD中，AB=BC=CD=DA=DB=AC,M、N分别为BC、AD的中点。 　 　求：AM与CN所成的角的余弦值； 解析：(1)连接DM,过N作NE∥AM交DM于E，则∠CNE 　为AM与CN所成的角。 　∵N为AD的中点, NE∥AM省　 　∴NE=AM且E为MD的中点。 　设正四面体的棱长为1，　则NC=·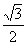= 且ME=MD= 　在Rt△MEC中，CE²=ME²+CM²=+=

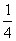∴cos∠CNE=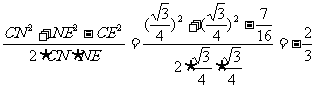, 　又∵∠CNE ∈(0, ) ∴异面直线AM与CN所成角的余弦值为.

注：1、本题的平移点是N，按定义作出了异面直线中一条的平行线，然后先在△CEN外计算CE、CN、EN长，再回到△CEN中求角。

50.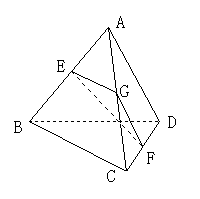 点A是BCD所在平面外一点，AD=BC，E、F分别是AB、CD的中点，且EF= 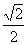AD，求异面直线AD和BC所成的角。(如图)　　　　　　

解析：设G是AC中点，连接DG、FG。因D、F分别是AB、CD中点，故EG∥BC且EG= BC，FG∥AD，且FG=AD，由异面直线所成角定义可知EG与FG所成锐角或直角为异面直线AD、BC所成角，即∠EGF为所求。由BC=AD知EG=GF=AD，又EF=AD_，由余弦定理可得cos∠EGF=0，即∠EGF=90°。

　　 注：本题的平移点是AC中点G，按定义过G分别作出了两条异面直线的平行线，然后在△EFG中求角。通常在出现线段中点时，常取另一线段中点，以构成中位线，既可用平行关系，又可用线段的倍半关系。

49. 设空间四边形ABCD，E、F、G、H分别是AC、BC、DB、DA的中点，若AB＝12，CD＝4 ，且四边形EFGH的面积为12 ，求AB和CD所成的角.

解析： 由三角形中位线的性质知，HG∥AB，HE∥CD，∴ ∠EHG就是异面直线AB和CD所成的角.

∵　 EFGH是平行四边形，HG＝ AB＝6，

HE＝ ，CD＝2，

∴　 S_EFGH＝HG·HE·sin∠EHG＝12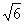 sin∠EHG,∴ 12 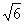sin∠EHG＝12.

∴　 sin∠EHG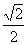＝,故∠EHG＝45°.

∴　 AB和CD所成的角为45°

注：本例两异面直线所成角在图中已给，只需指出即可。

48.经过平面外两点A，B和平面垂直的平面有几个？

解析：一个或无数多个。

当A，B不垂直于平面时，只有一个。

当A，B垂直于平面时，有无数多个。

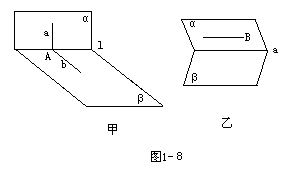
47. 画出满足下列条件的图形。

(1)α∩β=1，a α，b β，a∩b=A

(2)α∩β=a，b β，b∥a

解析：如图1-8-甲，1-8-乙

46. 三条平行直线可以确定平面_________个。答案：1个或3个

解析：分类、一类三线共面，即确定一个平面，另一类三线不共面，每两条确定一个，可确定3个。

45. 三角形、四边形、正六边形、圆，其中一定是平面图形的有________3个。

解析：三角形的三个顶点不在一条直线上，故可确定一个平面，三角形在这个平面内；圆上任取三点一定不在一条直线上，这三点即确定一个平面，也确定了这个圆所在的平面，所以圆是平面图形；而正六边形内接于圆，故正六边形也是平面图形；而四边形就不一定是平面图形了，它的四个顶点可以不在同一平面内。

44. 空间一条直线及不在这条直线上的两个点，如果连结这两点的直线与已知直线_______，则它们在同一平面内。答案：相交或平行

解析：根据推论2，推论3确定平面的条件。

43. 如果一条直线上有一个点不在平面上，则这条直线与这个平面的公共点最多有____1个。

解析：如果有两个，则直线就在平面内，那么直线上的所有点都在这个平面内，这就与已知有一个点不在平面上矛盾，所以这条直线与这个平面的公共点最多有一个。