
2.一机器狗每秒钟前进或后退一步,程序设计师让机器狗以前进3步然后再后退2步的规律移动.如果将此机器狗放在数轴的原点,面向正方向,以1步的距离为1个单位长,令P(n)表示第n秒时机器狗所在位置的坐标,且P(0)=0,那么下列结论中错误的是( )
A.P(3)=3 B.P(5)=1 C.P(101)=21 D.P(103)<P(104)
解析:P(3)=3,P(5)=1显然是正确的,机器狗的规律是5秒前进一步,故P(100)=20,那么P(101)=21,即第101秒正好是前进一步,错误的只有D.
答案:D
1.已知整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…则第60个数对是( )
A.(3,8) B.(4,7) C.(4,8) D.(5,7)
解析:观察可知横坐标和纵坐标之和为2的数对有1个,和为3的数对有2个,和为4的数对有3个,和为5的数对有4个,依此类推和为n+1的数对有n个,多个数对的排序是按照横坐标依次增大的顺序来排的,由=60⇒n(n+1)=120,n∈Z,n=10时,=55个数对,还差5个数对,且这5个数对的横、纵坐标之和为12,它们依次是(1,11),(2,10),(3,9),(4,8),(5,7),
所以第60个数对是(5,7).
答案:D
10.(1)找出三角形和空间四面体的相似性质;
(2)并用三角形的下列性质类比出四面体的有关性质.
①三角形的两边之和大于第三边.
②三角形的中位线等于第三边的一半,并且平行第三边.
③三角形的三条内角平分线交于一点,且这个点是三角形内切圆的圆心.
④三角形的面积为S=(a+b+c)r(r为内切圆半径).
解答:三角形和四面体有下列共同性质.
(1)三角形是平面内由直线段围成的最简单的封闭图形;四面体是空间中由平面三角形所围成的最简单的封闭图形.
(2)三角形可以看作平面上一条线段外一点及这条线段上的各点所形成的图形;四面体可以看作三角形外一点与这个三角形上各点的连线所围成的图形.
根据三角形的性质可以推测空间四面体有如下性质.
|
三角形 |
四面体 |
|
三角形的两边之和大于第三边 |
四面体任意三个面的面积之和大于第四个面的面积 |
|
三角形的中位线等于第三边的一半,并且平行于第三边 |
四面体的中位面的面积等于第四个面面积的,且平行于第四个面 |
|
三角形的三条内角平分线交于一点,且这个点是三角形内切圆的圆心 |
四面体的六个二面角的平分面交于一点,且这个点是四面体内切球的球心 |
|
三角形的面积为S=(a+b+c)r(r为三角形内切圆的半径) |
四面体的体积为V=(S1+S2+S3+S4)r,S1,S2,S3,S4为四个面的面积,r为内切球的半径 |
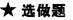
9.如右图所示,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EFcos∠DFE.
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
证明:(1)∵PM⊥BB1,PN⊥BB1,∴BB1⊥平面PMN.∴BB1⊥MN.
又CC1∥BB1,∴CC1⊥MN.
(2)在斜三棱柱ABC-A1B1C1中,有S2ABB1A1=S2BCC1B1+S2ACC1A1-2SBCC1B1SACC1A1cos α.
其中α为平面CC1B1B与平面CC1A1A所组成的二面角.
∵CC1⊥平面PMN,∴上述的二面角的平面角为∠MNP.
在△PMN中,PM2=PN2+MN2-2PN·MNcos∠MNP⇒
PM2·CC=PN2·CC+MN2·CC-2(PN·CC1)·(MN·CC1)cos∠MNP,
由于SBCC1B1=PN·CC1,SACC1A1=MN·CC1,
SABB1A1=PM·BB1=PM·CC1,∴有S2ABB1A1=S2BCC1B1+S2ACC1A1-2SBCC1B1·SACC1A1·cos α.
8.已知sin230°+sin290°+sin2150°=,sin25°+sin265°+sin2125°=.通过观察上述两个不等式的规律,请写出一个一般性的命题,并给出证明.
解答:一般性的命题为:sin2α+sin2(60°+α)+sin2(120°+α)=.
证明如下:
左边=++
=-[cos 2α+cos(120°+2α)+cos(240°+2α)]
=-[cos 2α+cos 120°cos 2α-sin 120°sin 2α+
cos 240°cos 2α-sin 240°sin 2α]==右边.
所以命题得证.
7.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2.设想正方形换成正方体,把截线换成如下图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是________.
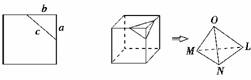
答案:S+S+S=S
6.设正数数列{an}前n项和为Sn,且存在正数t,使得对所有自然数n,有=,则通过归纳猜想可得到Sn=________.
解析:令n=1,则=,∴S1=a1=t.令n=2,则=,则a2=3t.
∴S2=4t.同理S3=9t.归纳Sn=n2t.
答案:n2t
5.中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.如果集合A中元素之间的一个关系“-”满足以下三个条件:
(1)自反性:对于任意a∈A,都有a-a;
(2)对称性:对于a,b∈A,若a-b,则有b-a;
(3)传递性:对于a,b,c∈A,若a-b,b-c,则有a-c,
则称“-”是集合A的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:________.
答案:答案不唯一,如“图形的全等”、“图形的相似”、“非零向量的共线”、“命题的充要条件”等等.
4.如下图所示,把1,3,6,10,15,21,…这些数叫做三角形数,这是因为这些数目的点可以排成一个正三角形,试求第七个三角形数是( )

A.27 B.28 C.29 D.30
解析:a1=1,a2=a1+2,a3=a2+3,a4=a3+4,∴an-an-1=n,
∴an=n+(n-1)+(n-2)+…+2+1=,∴a7==28.
答案:B
3.下列推理是归纳推理的是( )
A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆
B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式
C.由圆x2+y2=r2的面积πr2,猜出椭圆+=1的面积S=πab
D.科学家利用鱼的沉浮原理制造潜艇
解析:从S1,S2,S3猜想出数列的前n项和Sn,是从特殊到一般的推理,所以B是归纳推理.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com