1．(2010·梅州模拟)2009年当地时间9月23日，在位于印度安

得拉邦斯里赫里戈达岛的萨蒂什·达万航天中心，一枚PSLV

－C14型极地卫星运载火箭携带七颗卫星发射升空，成功实

现“一箭七星”发射，相关图片如图1所示．则下列说法不正　　　　　 图1

确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．火箭发射时，喷出的高速气流对火箭的作用力大于火箭对气流的作用力

B．发射初期，火箭处于超重状态，但它受到的重力却越来越小

C．高温高压燃气从火箭尾部喷出时对火箭的作用力与火箭对燃气的作用力大小相等

D．发射的七颗卫星进入轨道正常运转后，均处于完全失重状态

解析：由作用力与反作用力大小相等，可知A错误；火箭发射初期，因为火箭向上加速运动，故处于超重状态，随着火箭距地越来越远，所受的重力也越来越小，B正确；由作用力与反作用力的关系可知C正确；卫星进入轨道正常运转后，所受的万有引力充当向心力，此时各卫星均处于完全失重状态，D正确．

答案：A

(三)解答题

16、已知一个等比数列首项为1，项数是偶数，其奇数项之和为85，偶数项之和为170，求这个数列的公比和项数。

17、已知等比数列{a_n}的首项为a₁>0，公比q>-1(q≠1)，设数列{b_n}的通项b_n=a_n+1+a_n+2(n∈N₊)，数列{a_n},{b_n}的前n项和分别记为A_n，B_n，试比较A_n与B_n大小。

18、数列{a_n}中，a₁=8，a₄=2且满足a_n+2=2a_n+1-a_n(n∈N₊)

(1)求数列{a_n}通项公式；

(2)设S_n=|a₁|+|a₂|+…+|a_n|，求S_n；

(3)设(n∈N₊)T_n=b₁+b₂+…+b_n，是否存在最大的整数m，使得对于任意的n∈N₊，均有成立？若存在，求出m的值；若不存在，说明理由。

(二)　　　 填空题

11、已知数列{a_n}满足a₁+2a₂+3a₃+…+na_n=n(n+1)(n+2)，则它的前n项和S_n=______。

12、设等差数列{a_n}共有3n项，它的前2n项之和为100，后2n项之和为200，则该等差数列的中间n项的和等于

________。

13、设数列{a_n}，{b_n}(b_n>0)，n∈N₊满足(n∈N₊)，则{a_n}为等差数列是{b_n}为等比数

列的________条件。

14、长方体的三条棱成等比数列，若体积为216cm³，则全面积的最小值是______cm²。

15、若不等于1的三个正数a，b，c成等比数列，则(2-log_ba)(1+log_ca)=________。

(一)　　　 选择题

　　 1、已知a，b，a+b成等差数列，a，b，ab成等比数列，且0<log_mab<1，则m取值范围是

A、m>1　　　　　 　　　　 B、1<m<8　　　　 　　　　 C、m>8　　　　 　　　　 D、0<m<1或m>8

2、设a>0，b>0，a，x₁，x₂，b成等差数列，a，y₁，y₂，b成等比数列，则x₁+x₂与y₁+y₂的大小关系是

A、x₁+x₂≤y₁+y₂　　　　　 B、x₁+x₂≥y₁+y₂ C、x₁+x₂<y₁+y₂　　　　　 　D、x₁+x₂>y₁+y₂

3、已知S_n是{a_n}的前n项和，S_n=Pⁿ(P∈R，n∈N_+­­)，那么数列{a_n}

A、　 是等比数列　　　　　　　　　　　 　　　　　　 B、当P≠0时是等比数列

C、　 当P≠0，P≠1时是等比数列　　　　 　　　　　　 D、不是等比数列

4、{a_n}是等比数列，且a_n>0，a₂a₄+2a₃a₅+a₄a₆=25，则a₃+a₅等于

A、5　　　　　　　 　　 B、10　　　　　　 　　　 C、15　　　　　　　 D、20

5、已知a，b，c成等差数列，则二次函数y=ax²+2bx+c的图象与x轴交点个数是

A、　 0　　　　　　　 　　　 B、1　　　　　　　 　　　 C、2　　　　　　　 　 D、1或2

6、设m∈N₊，log₂m的整数部分用F(m)表示，则F(1)+F(2)+…+F(1024)的值是

A、　 8204　　　　　 　　　 B、8192　　　　　 　　　 C、9218　　　　　 　 D、8021

　　 7、若x的方程x²-x+a=0和x²-x+b=0(a≠b)的四个根可组成首项为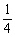的等差数列，则a+b的值为

A、　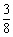 　　　　　　　　　 B、　　　　　　 　　　 C、　　　　　 　　 D、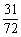

8、　 在100以内所有能被3整除但不能被7整除的正整数和是

A、1557　　　　　 　　　 B、1473　　　　　　 　　 C、1470　　　　　 　 D、1368

　　 9、从材料工地运送电线杆到500m以外的公路，沿公路一侧每隔50m埋栽一根电线杆，已知每次最多只能运3根，要完成运载20根电线杆的任务，最佳方案是使运输车运行

A、　 11700m　　　　 　　　 B、14700m　　　　　 　　 C、14500m　　　　 　 D、14000m

　　 10、已知等差数列{a_n}中，|a₃|=|a₉|，公差d<0，则使前n项和S_n取最大值的正整数n是

A、4或5　　　　　 　　 B、5或6　　　　　 　　 C、6或7　　　　 　 D、8或9

　 　例1、已知数列{a_n}为等差数列，公差d≠0，其中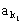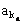，，…，恰为等比数列，若k₁=1，k₂=5，k₃=17，求k₁+k₂+…+k_n。

解题思路分析：

从寻找新、旧数列的关系着手

设{a_n}首项为a₁，公差为d

∵ a₁，a₅，a₁₇成等比数列

∴ a₅²=a₁a₁₇

∴(a₁+4d)²=a₁(a₁+16d)

∴ a₁=2d

设等比数列公比为q，则

对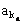项来说，

在等差数列中：

在等比数列中：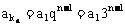

∴

∴

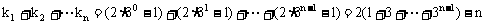
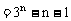
注：本题把k₁+k₂+…+k_n看成是数列{k_n}的求和问题，着重分析{k_n}的通项公式。这是解决数列问题的一般方法，称为“通项分析法”。

例2、设数列{a_n}为等差数列，S_n为数列{a_n}的前n项和，已知S₇=7，S₁₅=75,T_n为数列{}的前n项和，求T_n。

解题思路分析：

法一：利用基本元素分析法

设{a_n}首项为a₁，公差为d，则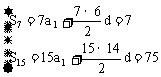

∴

∴

∴

此式为n的一次函数

∴ {}为等差数列

∴

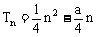
法二：{a_n}为等差数列，设S_n=An²+Bn

∴

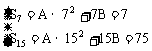
解之得：

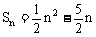∴ ，下略

注：法二利用了等差数列前n项和的性质

例3、正数数列{a_n}的前n项和为S_n，且，求：

(1)数列{a_n}的通项公式；

(2)设，数列{b_n}的前n项的和为B_n，求证：B_n.

解题思路分析：

(I)涉及到a_n及S_n的递推关系，一般都用a_n=S_n-S_n-1(n≥2)消元化归。

∵

∴ 4S_n=(a_n+1)²

∴ 4S_n-1=(a_n-1+1)²(n≥2)

∴ 4(S_n-S_n-1)=(a_n+1)²-(a_n-1+1)²

∴ 4a_n=a_n²-a_n-1²+2a_n-2a_n-1

整理得：(a_n-1+a_n)(a_n-a_n-1-2)=0

∵ a_n>0

∴ a_n-a_n-1=2

∴ {a_n}为公差为2的等差数列

在中，令n=1，a₁=1

∴ a_n=2n-1

　 (II)

∴

注：递推是学好数列的重要思想，例本题由4S_n=(a_n+1)²推出4S_n-1=(a_n-1+1)²，它其实就是函数中的变量代换法。在数列中一般用n-1，n+1等去代替n，实际上也就是说已知条件中的递推关系是关于n的恒等式，代换就是对n赋值。

例4、等差数列{a_n}中，前m项的和为77(m为奇数)，其中偶数项的和为33，且a₁-a_m=18，求这个数列的通项公式。

解题思路分析：

利用前奇数项和和与中项的关系

令m=2n-1，n∈N₊

则

∴

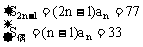
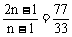
∴ n=4

∴ m=7

∴ a_n=11

∴ a₁+a_m=2a_n=22

又a₁-a_m=18

∴ a₁=20，a_m=2

∴ d=-3

∴ a_n=-3n+23

例5、设{a_n}是等差数列，，已知b₁+b₂+b₃=，b₁b₂b₃=，求等差数列的通项a_n。

解题思路分析：

∵ {a_n}为等差数列

∴ {b_n}为等比数列

从求解{b_n}着手

∵ b₁b₃=b₂²

∴ b₂³=

∴ b₂=

∴

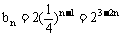∴ 　或

∴ 　或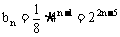

∵

∴

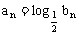
∴ a_n=2n-3 或 a_n=-2n+5

注：本题化归为{b_n}求解，比较简单。若用{a_n}求解，则运算量较大。

例6、已知{a_n}是首项为2，公比为的等比数列，S_n为它的前n项和，

(1)用S_n表示S_n+1；

(2)是否存在自然数c和k，使得成立。

　　 解题思路分析：

　 (1)∵

∴

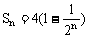
　 (2)(*)

∵

∴

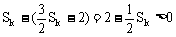
∴ 式(*)　　　 ①

∵ S_k+1>S_k

∴

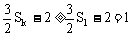
又S_k<4

∴ 由①得：c=2或c=3

当c=2时

∵ S₁=2

∴ k=1时，c<S_k不成立，从而式①不成立

∵

∴ 由S_k<S_k+1得：

∴ 当k≥2时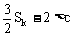，，从而式①不成立

　 当c=3时，S₁2，S₂=3

∴ 当k=1，2时，C<S_k不成立

∴ 式①不成立

∵

∴ 当k≥3时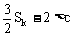，，从而式①不成立

综上所述，不存在自然数c，k，使成立

例7、某公司全年的利润为b元，其中一部分作为资金发给n位职工，资金分配方案如下：首先将职工按工作业绩(工作业绩均不相等)从大到小，由1到n排序，第1位职工得资金元，然后再将余额除以n发给第2位职工，按此方法将资金逐一发给每位职工，并将最后剩余部分作为公司发展基金。

　 (1)设a_k(1≤k≤n)为第k位职工所得资金额，试求a₂，a₃，并用k，n和b表示a_k(不必证明)；

　 (2)证明：a_k<a_k+1(k=1，2，…，n-1)，并解释此不等式关于分配原则的实际意义。

解题思路分析：

谈懂题意，理清关系，建立模型

第1位职工的奖金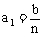

第2位职工的奖金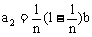

第3位职工的奖金

……

第k位职工的奖金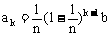

　 (2)

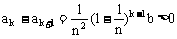
此奖金分配方案体现了“按劳分配”或“不吃大锅饭”等原则。

例8、试问数列{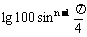}的前多少项的和最大，并求这个最大值(lg2=0.3010)

解题思路分析：

法一：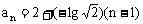

∴ {a_n}为首项为2，公差为的等差数列

∴

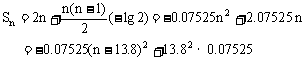
∵ n∈N₊

∴ n=14时，(S_n)_max=14.35

法二：∵ a₁=2>0，d=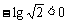

∴ {a_n}是递减数列，且S_n必为最大值

设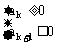

∴

∴

∴ k=14

∴ (S_n)_max=S₁₄=14.35

4、等差、等比数列的应用

　 (1)基本量的思想：常设首项、公差及首项，公比为基本量，借助于消元思想及解方程组思想等；

　 (2)灵活运用等差数列、等比数列的定义及性质，简化计算；

　 (3)若{a_n}为等差数列，则{}为等比数列(a>0且a≠1)；

若{a_n}为正数等比数列，则{log_aa_n}为等差数列(a>0且a≠1)。

3、等比数列

(1)定义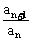：=q(q为常数，a_n≠0)；a_n²=a_n-1a_n+1(n≥2，n∈N₊)；

(2)通项公式：a_n=a₁q^n-1，a_n=a_mq^n-m;

　　 前n项和公式：；

(3)性质

当m+n=p+q时，a_ma_n=a_pa_q，特例：a₁a_n=a₂a_n-1=a₃a_n-2=…，当2n=p+q时，a_n²=a_pa_q，数列{ka_n}，{}成等比数列。

2、等差数列

　 (1)定义，{a_n}为等差数列a_n+1-a_n=d(常数)，n∈N₊2a_n=a_n-1+a_n+1(n≥2，n∈N₊)；

　 (2)通项公式：a_n=a_n+(n-1)d，a_n=a_m+(n-m)d；

　　　　 前n项和公式：；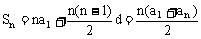

　 (3)性质：a_n=an+b，即a_n是n的一次型函数，系数a为等差数列的公差；

　　 S_n=an²+bn，即S_n是n的不含常数项的二次函数；

若{a_n}，{b_n}均为等差数列，则{a_n±n_n},{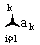},{ka_n+c}(k，c为常数)均为等差数列；

当m+n=p+q时，a_m+a_n=a_p+a_q，特例：a₁+a_n=a₂+a­_n-1=a₃+a_n-2=…；当2n=p+q时，2a_n=a_p+a_q；

当n为奇数时，S_2n-1=(2n-1)a­_n；S_奇=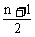a_中，S_偶=a_中。

1、数列，是按照一定顺序排列而成的一列数，从函数角度看，这种顺序法则就是函数的对应法则，因此数列可以看作是一个特殊的函数，其特殊性在于：第一，定义域是正整数集或其子集；第二，值域是有顺序的，不能用集合符号表示。

研究数列，首先研究对应法则——通项公式：a_n=f(n)，n∈N₊，要能合理地由数列前n项写出通项公式，其次研究前n项和公式S_n：S_n=a₁+a₂+…a_n，由S_n定义，得到数列中的重要公式：。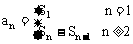

一般数列的a_n及S_n,，除化归为等差数列及等比数列外，求S_n还有下列基本题型：列项相消法，错位相消法。

2、一般数列的通项及前n项和计算。