
3.设f (x)=x2-4x (x∈R),则f (x)>0的一个必要而不充分条件是 ( )
A、x<0 B、x<0或x>4
C、│x-1│>1 D、│x-2│>3
[填空题]
2.(2004重庆)一元二次方程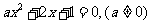 有一个正根和一个负根的充分不必要条件是
( )
有一个正根和一个负根的充分不必要条件是
( )
(A)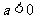 (B)
(B)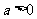 (C)
(C)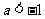 (D)
(D)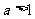
1. 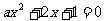 至少有一个负的实根的充要条件是( )
至少有一个负的实根的充要条件是( )
A
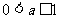 B
B
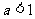 C
C
 D
D
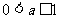 或
或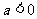
2.题型.思想.方法:
(1)二次函数在闭区间上,必有最大值和最小值,当含有参数时,须对参数分区间讨论。
(2)二次方程根的分布问题,可用韦达定理或借助二次函数图象列不等式组求解。
(3)三个二次问题(二次函数、二次方程、二次不等式)是中学数学中基础问题,以函数为核心,三者密切相连。
例题简答
同步练习 1.4 二次函数 方程 不等式
[选择题]
1.二次函数f(x)=ax2+bx+c(a≠0)的图象性质是处理二次函数问题的重要依据。
[例1]已知方程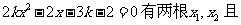
(1)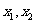 都小于零; (2)都小于1;
都小于零; (2)都小于1;
(3)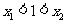 ;
(4)
;
(4)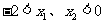
(5)恰有一根在(1,2)区间内。
分别求k的取值范围。
解法1:利用韦达定理
(1) 由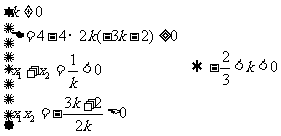 ;
;
(2) 由

特别提示:不能由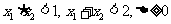 来求解。
来求解。
…………
解法2:利用二次函数的图象
…………
(3)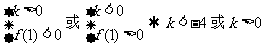
(4)
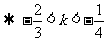
(5)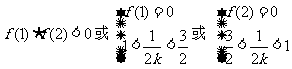

[例2]设f(x)=x2-2ax+2.当x∈[-1,+∞)时,f(x)≥a恒成立,求实数a的取值范围
解:(1)当对称轴x=a≤-1时,f(x)min=f(-1)=3+2a.
x∈[-1,+∞),f(x)≥a恒成立
f(x)min=3+2a≥a a≥-3.故此时-3≤a≤-1.
a≥-3.故此时-3≤a≤-1.
当a>-1时,f(x)min=f(a)=a2-2a2+2=2-a2,
x∈[-1,+∞),f(x)≥a恒成立 f(x)min=2-a2≥a
f(x)min=2-a2≥a -2≤a≤1.故此时-1<a≤1.
-2≤a≤1.故此时-1<a≤1.
由(1)(2)知,当-3≤a≤1时,x∈[-1,+∞),f(x)≥a恒成立.
[例3](2005全国卷Ⅰ)已知二次函数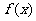 的二次项系数为
的二次项系数为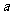 ,且不等式
,且不等式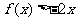 的解集为
的解集为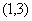 。(Ⅰ)若方程
。(Ⅰ)若方程 有两个相等的根,求
有两个相等的根,求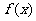 的解析式;
的解析式;
(Ⅱ)若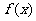 的最大值为正数,求
的最大值为正数,求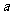 的取值范围。
的取值范围。
解:(Ⅰ)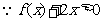 的解集为(1,3),
的解集为(1,3),
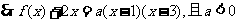
∴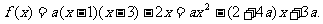 ①
①
由方程 ②
②
∵方程②有两个相等的根,∴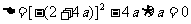 ,
,
即 
 代入①得
代入①得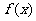 的解析式
的解析式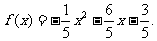
(Ⅱ)由
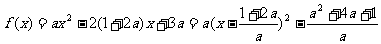 及
及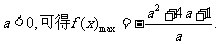 由
由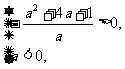
解得: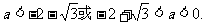
故当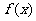 的最大值为正数时,实数a的取值范围是
的最大值为正数时,实数a的取值范围是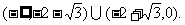
法2:由Δ>0求解。
[例4](2006浙江)设f(x)=3ax2+2bx+c,若a+b+c=0, ,f(0)>0,f(1)>0,求证:
(Ⅰ)a>0且-2<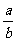 <-1;(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
<-1;(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
证明:(I)因为f(0)>0,f(1)>0,所以c>0,3a+2b+c>0
由条件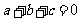 ,消去
,消去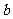 ,得
,得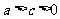 ;
;
由条件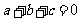 ,消去
,消去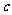 ,得
,得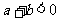 ,
, .
.
故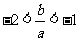 .
.
(II)抛物线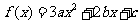 的顶点坐标为
的顶点坐标为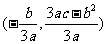 ,
,
在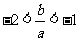 的两边乘以
的两边乘以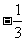 ,得
,得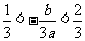 .
.
又因为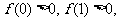
而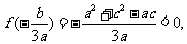
所以方程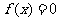 在区间
在区间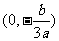 与
与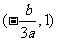 内分别有一实根
内分别有一实根
故方程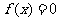 在
在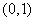 内有两个实根.
内有两个实根.
[研究.欣赏]已知二次函数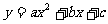 的图像经过(-1,0),是否存在常数
的图像经过(-1,0),是否存在常数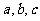 使得不等式
使得不等式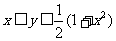 对一切实数
对一切实数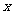 都成立?若存在,求出
都成立?若存在,求出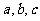 ;若不存在,说明理由
;若不存在,说明理由
解: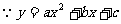 的图像经过点(-1,0),
的图像经过点(-1,0),
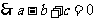
又 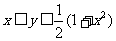 ,令
,令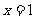
得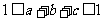 ,即
,即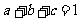
由上式得: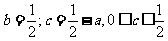
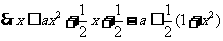
即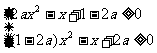 的解为
的解为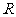
(1)当
(2)当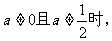
 不等式组的解为
不等式组的解为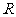 ;
;
当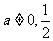 时,由
时,由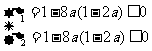
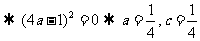
因此存在常数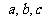 ,其中
,其中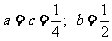

4.设u=x2-1,化原式为: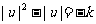 ,结合函数
,结合函数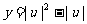 的图象,看使u≥-1的解的个数
的图象,看使u≥-1的解的个数
3.对称轴为x=2;
2.顶点为(a+b,c2-a2-b2),由已知c2-a2-b2=0.∴Rt△
1.对称轴 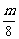 ≤-2
≤-2 m≤-16,∴f(1)=9-m≥25.
m≤-16,∴f(1)=9-m≥25.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com