
2.下列现象属于波的干涉的是( )
A.夏天里在一次闪电过后,有时雷声轰鸣不绝
B.“闻其声而不见其人”
C.学生围绕振动的音叉转一圈会听到忽强忽弱的声音
D.当正在鸣笛的火车向着我们急驶而来时,我们听到汽笛声的音调变高。这些物理现象 分别属于波的
1.下列所给光中,光子能量最大的是( )
A.红光 B.黄光 C .蓝光 D.紫光
10.设二次函数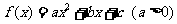 ,方程
,方程
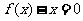 的两根
的两根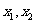 满足
满足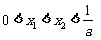
(1)
当 时,证明
时,证明
(2)
设函数 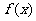 的图象关于
的图象关于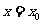 对称,证明
对称,证明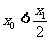 .
.
证明:
(1)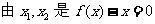 的根知
的根知
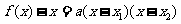
由已知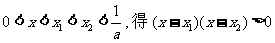 又
又
故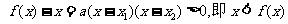
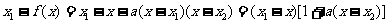
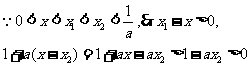
得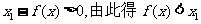
(2)依题意知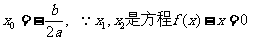
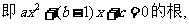
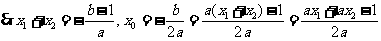
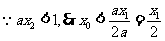
法2:
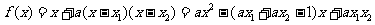
对称轴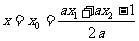 ……
……
[探索题]1.设函数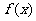 =
=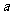 x2+8x+3 (
x2+8x+3 (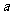 <0),对于给定的负数
<0),对于给定的负数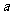 ,有一个最大的正数
,有一个最大的正数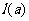 ,使得在整个区间[0,
,使得在整个区间[0,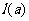 ]上,不等式|
]上,不等式|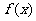 |≤5都成立。问
|≤5都成立。问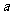 为何值时
为何值时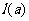 最大?求出这个最大的
最大?求出这个最大的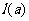 ,证明你的结论。
,证明你的结论。
[解法]: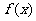 =
=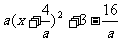 ,∵
,∵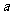 <0∴
<0∴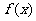 max=
max=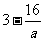
当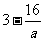 >5,即-8<
>5,即-8<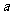 <0时,0<
<0时,0<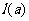 <-
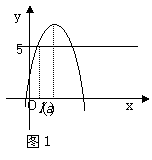
<-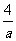 (如图1)
(如图1)
∴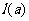 是方程
是方程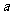 x2+8x+3=5的较小根
x2+8x+3=5的较小根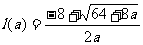 =
=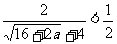

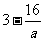 ≤5,即
≤5,即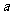 ≤-8时,
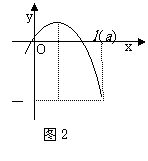
≤-8时,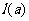 >-
>-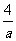 (如图2)
(如图2)
∴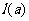 是方程
是方程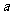 x2+8x+3=-5的较大根
x2+8x+3=-5的较大根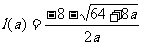 =
=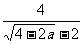
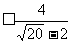 =
=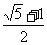 ,当且仅当
,当且仅当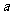 =-8时等号成立,由于
=-8时等号成立,由于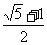 >
>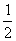 ,
,
因此当且仅当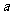 =-8时,
=-8时,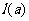 取最大值
取最大值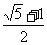 。
。
点评:本题是典型的函数、方程、不等式的综合问题,数形结合利于开拓思路,找到解决办法。
9.对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0)(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
解:(1)当a=1,b=-2时,f(x)=x2-x-3=x x2-2x-3=0
x2-2x-3=0 (x-3)(x+1)=0
(x-3)(x+1)=0 x=3或x=-1,∴f(x)的不动点为x=3或x=-1.
x=3或x=-1,∴f(x)的不动点为x=3或x=-1.
(2)对任意实数b,f(x)恒有两个相异不动点
 对任意实数b,ax2+(b+1)x+b-1=x即ax2+bx+b-1=0恒有两个不等实根
对任意实数b,ax2+(b+1)x+b-1=x即ax2+bx+b-1=0恒有两个不等实根 对任意实数b,Δ=b2-4a(b-1)>0恒成立
对任意实数b,Δ=b2-4a(b-1)>0恒成立
 对任意实数b,b2-4ab+4a>0恒成立
对任意实数b,b2-4ab+4a>0恒成立
 Δ′=(4a)2-4×4a<0
Δ′=(4a)2-4×4a<0 0<a<1.
0<a<1.
8. 已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx,其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)。
(1)求证:两函数的图象交于不同的两点A、B;
(2)求线段AB在x轴上的射影A1B1的长的取值范围。
证明(1)
由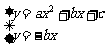 消去y得ax2+2bx+c=0
消去y得ax2+2bx+c=0
Δ=4b2-4ac=4(-a-c)2-4ac=4(a2+ac+c2)
=4[(a+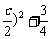 c2]
c2]
∵a+b+c=0,a>b>c,∴a>0,c<0
∴ c2>0,∴Δ>0,即两函数的图象交于不同的两点。
c2>0,∴Δ>0,即两函数的图象交于不同的两点。
解(2) 设方程ax2+bx+c=0的两根为x1和x2,则
x1+x2=-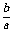 ,x1x2=
,x1x2=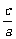 。|A1B1|2=(x1-x2)2=(x1+x2)2-4x1x2
。|A1B1|2=(x1-x2)2=(x1+x2)2-4x1x2

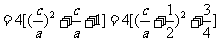
∵a>b>c,a+b+c=0,a>0,c<0
∴a>-a-c>c,解得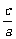 ∈(-2,-
∈(-2,-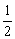 )
)
∵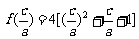 的对称轴方程是
的对称轴方程是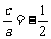
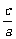 ∈(-2,-
∈(-2,-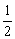 )时,为减函数
)时,为减函数
∴|A1B1|2∈(3,12),故|A1B1|∈( )
)
7.已知关于x的二次方程x2+2mx+2m+1=0
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的取值范围。
(2)若方程两根在区间(0,1)内,求m的范围。
思维分析:一般需从三个方面考虑①判别式Δ②区间端点函数值的正负③对称轴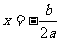 与区间相对位置。
与区间相对位置。
解:设f (x)=x2+2mx+2m+1
(1)由题意 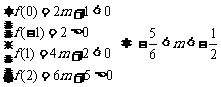
(2) 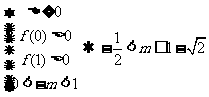
6、画二次函数图象知m∈[1,2].
[解答题]
6.已知f(x)=x2-2x+3,在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是___________________.
答案:1-3、CCC;4、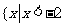 或
或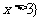 ;5、2; 6、[1,2]
;5、2; 6、[1,2]
提示:1、排除法
当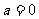 时,原方程有一个负的实数,可以排除A、D
时,原方程有一个负的实数,可以排除A、D
当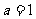 时,原方程有两个相等的负实数,可以排除B,故选C
时,原方程有两个相等的负实数,可以排除B,故选C
5. (2005江苏)已知a,b为常数,若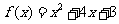 ,
,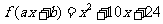 则
则 .
.
4.(2004江苏)二次函数y=ax2+bx+c (x∈R)的部分对应值如下表:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
则不等式ax2+bx+c>0的解集是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com