
重点:应用数学理论解决实际问题的兴趣培养和能力提升
难点:函数建模及应用函数探求问题的能力培养.
3.情感、态度与价值观
在实际问题求解的过程中,享受数学为人们的生产和生活服务的乐趣,激发学生学习数学知识的兴趣.
2.进程与方法
在实例分析、解决的过程中,体会函数增长快慢的实际意义,从而提高学生应用数学解决实际问题的能力.
1.知识与技能
利用函数增长的快慢一般规律,借助函数模型,研究解决实际问题,培养数学的应用意识.
合作交流与知识讲授相结合,通过学习熟悉的几种常见函数增长快慢的比较,体会比较方法,掌握基本结论,从而培养应用基本方法比较函数增长快慢的能力.
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
提出问题引入课题 |
观察函数 在
[0,+∞)上的图象,说明在不同区间内,函数增长的快慢情况. 在
[0,+∞)上的图象,说明在不同区间内,函数增长的快慢情况. 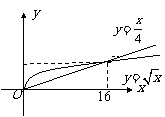 在同一坐标中函数图象如下 在同一坐标中函数图象如下   结论:若0<x<16则  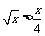  若x>16则 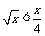 |
师:增函数的共同特点是函数值y随自变量x的增长而增长,但不同函数在同一区间内的增长快慢是否相同? 师生合作观察研究函数  的增长快慢. 的增长快慢. ①x∈(0,16)时, 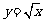 的图象在 的图象在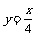 图象上方 图象上方 可知 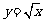 增长较快 增长较快 ② 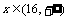 时, 时,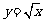 的图在 的图在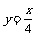 图象下方, 图象下方, 可知 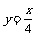 增长较快 增长较快 |
由问题引入课题,激发学习兴趣. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
幂、指对函数增长快慢比较形成比较方法. |
1.实例探究: 比较函数y=2x,y= x2,y = log2x的增长快慢.  方法:①作图,列表比较、验证  ②应用二分法求2x = x2的根,即y = 2x与y = x2的交点横坐标.  2.规律总结  ①一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>0),在区间 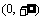 上,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn. 上,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn. ②对于对数函数y=logax(a>1)和幂函数y = xn(n>0)在区间 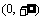 上,随着x的增大,logax增长得越来越慢.在x的一定变化范围内,logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax<xn. 上,随着x的增大,logax增长得越来越慢.在x的一定变化范围内,logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax<xn. ③在区间 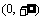 上,尽管函数y = ax(a>1),y = logax(a>1)和y = xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着x的增长,y = ax(a>1)的增长速度越来越快,会超过并远远大于y = xn(n>0)的增长速度,而y = logax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x>x0时,就有logax<xn<ax. 上,尽管函数y = ax(a>1),y = logax(a>1)和y = xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着x的增长,y = ax(a>1)的增长速度越来越快,会超过并远远大于y = xn(n>0)的增长速度,而y = logax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x>x0时,就有logax<xn<ax. |
师生合作:借助计算机作图,列表,进行探究 ①列表 
②作图
③结论 x∈R时log2x<x2,且log2x<2x. 进一步探究y = x2与y = 2x的增长快慢. ①列表
②作图
③结论x∈(0,2)时2x>x2,x∈(2,4)时,2x<x2,x∈ |
由特殊到一般探究规律 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
巩固练习 |
在同一平面直角坐标系内作出下列函数的图象,并比较它们的增长情况: (1)y=0.1ex–100,x∈[1,10]; (2)y=20lnx+100,x∈[1,10]; (3)y=20x, x∈[1,10]. |
三个函数图象如下: 由图象可以看到,函数(1)以“爆炸”式的速度增长;函数(2)增长缓慢,并渐渐趋于稳定;函数(3)以稳定的速率增加. |
进一步熟悉函数增长快慢的比较方法及步骤. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
课后作业 |
3.2 第一课时 习案 |
学生独立完成 |
巩固知识,培养能力 |
备选例题
例1 某人现在一笔资金x万元用于投资,经过市场调查研究,有三种方案:
第一种方案:存入银行,年利润Q1 = 0.018x;
第二种方案:借给朋友投资,年利润Q2 = 0.02x + 0.2;
第三种方案:办工厂,年利润Q3 = 0.2x2 + 2x – 35;
问:(1)投资4万元,选择哪种投资方案.
(2)投资10万元,选择哪种投资方案.
[解析] (1)投资4万元,则有:
Q1 = 0.072;Q2 = 0.28;Q3 = – 23.8,
∴Q2>Q1>Q3
∴选择第二种方案
(2)投资10万元,则有:Q1 = 0.18;Q2 = 0.4;Q3 = 5,
∴Q3>Q2>Q1,
∴选择第三种方案.
例2 为了发展电信事业方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“便民卡”与“如意卡”在某市范围每月(30天)的通话时间x(分),与通话费y(元)的关系如图所示.
|
|

(1)分别求出通话费y1, y2与通话时间x之间的函数关系式;
(2)请帮助用户计算,在一个月内使用哪种卡便宜.
[分析](1)由图象可设y1 = k1x +29,y2 = k2x,把点B (30, 35),C (30, 15)分别代入y1,y2得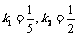 .
.
∴ .
.
(2)令y1 = y2,即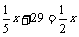 ,则
,则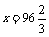 .
.
当x = 96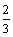 时,y1 = y2,两种卡收费一致;
时,y1 = y2,两种卡收费一致;
当x<96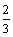 时,y1>y2,即如意卡便宜;
时,y1>y2,即如意卡便宜;
当x>96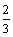 时,y1<y2,即便民卡便宜.
时,y1<y2,即便民卡便宜.
[评析]本题中的图形为直线,这就说明变量x,y之间满足一次函数关系,为此可采取待定系数法,求出具体的函数关系式,最后运用方程的思想求出关键点从而使问题得以解决. 图表题目的处理关键就在于正确理解其全部信息,运用合理的方法解决问题.
重点:函数增长快慢比较的常用途径;
难点:了解影响函数增长快慢的因素.
3.情感、态度与价值观
通过几种常见函数增长快慢的比较,感受“绝对与相对”的内涵和处延,培养思维的发散性.
2.过程与方程
利用函数图象,借助计算机列出自变量和函数值的对照表,比较几种常用函数增长的快慢,从而熟知常见函数增长快慢的一般性结论.
1.知识与技能
(1)掌握几种常用函数增长快慢的比较方法
(2)熟悉几种常用函数增长快慢的一般规律
15.五块完全相同的长木板依次紧挨着放在水平地面上,每块木板的长度为0.5m,质量为0.6 kg。在第一块长木板的最左端放置一质量为0.98 kg的小物块。已知小物块与长木板间的动摩擦因数为0.2,长木板与地面间的动摩擦因数为0.1,设最大静摩擦力与滑动摩擦力相等。一颗质量为0.02 kg的子弹以的150 m/s水平速度击中小物块并立即与小物块一起在长木板表面滑行,重力加速度g取10 m/s2。
(1)分析小物块滑至哪块长木板时,长木板才开始在地面上滑动。
(2)求物块在整个运动过程中相对出发点滑行的最大距离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com