
2.过程与方法
经历实际应用问题的求解过程,体验指数函数模型、拟合函数模型的题型特征,学会运用函数知识解决实际问题.
1.知识与技能
掌握应用指数型,拟合型函数模型解答实际应用问题的题型特征,提升学生解决简单的实际应用问题的能力.
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|||||||||||||||||||||||||||||||
|
复习引入 |
回顾一次函数和二次函数的有关知识. |
教师提出问题,学生回答. 师:一次函数、二次函数的解析式及图象与性质.  生:回答上述问题. |
以旧引新,激发兴趣. |
|||||||||||||||||||||||||||||||
|
应用举例 |
1.一次函数模型的应用 例1 某列火车从北京西站开往石家庄,全程277km.火车出发10min开出13km后,以120km/h的速度匀速行驶.试写出火车行驶的总路程S与匀速行驶的时间t之间的关系,并求火车离开北京2h内行驶的路程. |
教师提出问题,让学生读题,找关键字句,联想学过的函数模型,求出函数关系式.学生根据要求,完成例1的解答. 例1 解:因为火车匀速运动的时间为(200 – 13)÷120 = 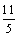 (h), (h), 所以 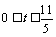 . . 因为火车匀速行驶时间t h所行驶路程为120t,所以,火车运行总路程S与匀速行驶时间t之间的关系是  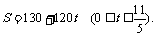  2h内火车行驶的路程 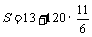 =233(km). =233(km). |
通过此问题背景,让学生恰当选择相应一次函数模型解决问题,加深对函数概念本质的认识和理解.让学生体验解决实际问题的过程和方法. |
|||||||||||||||||||||||||||||||
解题方法: 1.读题,找关键点;  2.抽象成数学模型;  3.求出数学模型的解;  4.做答. |
学生总结,教师完善. |
培养学生分析归纳、概括能力.从而初步体验解应用题的规律和方法. |
||||||||||||||||||||||||||||||||
2.二次函数模型的应用 例2 某农家旅游公司有客房300间,每间日房租20元,每天都客满.公司欲提高档次,并提高租金.如果每间客房每日增加2元,客房出租数就会减少10间.若不考虑其他因素,旅社将房间租金提高到多少时,每天客房的租金总收入最高? |
让学生自己读题,并回答下列问题: ①题目求什么,应怎样设未知量;  ②每天客房的租金收入与每间客房的租金、客房的出租数有怎样的关系;  ③学生完成题目.  法一:用列表法求解.此法可作为学生探求思路的方法,但由于运算比较繁琐,一般不用,应以法二求解为重点.对法二让学生读题,回答问题.教师指导,学生自己动手解题.  师生合作由实际问题建模,让学生尝试解答.  例2 解答:方法一 依题意可列表如下: 
由上表容易得到,当x = 10,即每天租金为40元时,能出租客房200间,此时每天总租金最高,为8000元.再提高租金,总收入就要小于8000元了. 方法二 设客房租金每间提高x个2元,则将有10x间客房空出,客房租金的总收入为 y = (20 + 2x) (300 – 10x ) = –20x2 + 600x –
200x + 6000 = –20(x2 – 20x +
100 – 100) + 6000 = –20(x
– 10)2 + 8000. 由此得到,当x = 10时,ymax = 8000.即每间租金为20 + 10×2
= 40(元)时,客房租金的总收入最高,每天为8000元. |
解应用题首先要读懂题意,设计出问题指导学生审题,建立正确的数学模型.同时,培养学生独立解决问题的能力. |
||||||||||||||||||||||||||||||||
|
|
3.分将函数模型的应用 例3 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.  (1)求图中阴影部分的面积,并说明所求面积的实际含义;  (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读数skm与时间th的函数解析式,并作出相应的图象.   |
生:解答: (1)阴影部分的面积为  50×1+80×1+90×1+75×1+65×1=360.  阴影部分的面积表示汽车在这5小时内行驶的路程为360km.  (2)根据图,有  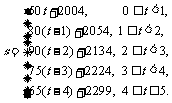  这个函数的图象如图所示.   |
实际应用用问题解决的一般步骤:理解问题 简化假设 简化假设 数学建模 数学建模 解答模型 解答模型 检验模型 检验模型 评价与应用的进一步深体. 评价与应用的进一步深体. |
|||||||||||||||||||||||||||||||
|
巩固练习 |
课堂练习 习题1.如果一辆汽车匀速行驶,1.5h行驶路程为90km,求这辆汽车行驶路程与时间之间的函数关系,以及汽车3h所行驶的路程.  习题2.已知某食品5kg价格为40元,求该食品价格与重量之间的函数关系,并求8kg食品的价格是多少元.  习题3.有300m长的篱笆材料,如果利用已有的一面墙(设长度够用)作为一边,围成一块矩形菜地,问矩形的长、宽各为多少时,这块菜地的面积最大?  习题4.某市一种出租车标价为1.20元/km,但事实上的收费标准如下:最开始4km内不管车行驶路程多少,均收费10元(即起步费),4km后到15km之间,每公里收费1.20元,15km后每公里再加收50%,即每公里1.80元.试写出付费总数f与打车路程x之间的函数关系. |
学生练习,师生点评. 1.设汽车行驶的时间为t h,则汽车行驶的路程Skm与时间t h之间的函数关系为 S = vt. 当t = 1.5时,S = 90,则v = 60. 因此所求的函数关系为S=60t, 当t = 3时,S = 180, 所以汽车3h所行驶的路程为180km. 2.设食品的重量为xkg,则食品的价格y元与重量xkg之间的函数关系式为y=8x,当x = 8时,y = 64, 所以当8kg食品的价格为64元. 3.设矩形菜地与墙相对的一边长为xcm,则另一组对边的长为 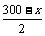 m,从而矩形菜地的面积为: m,从而矩形菜地的面积为: 当x = 150时,Smax = 11250. 即当矩形的长为150m,宽为75m时,菜地的面积最大. 4.解:所求函数的关系式为 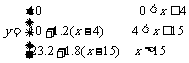 |
学生动手实践、体验所学方法,从而提升解应用题的技能. |
|||||||||||||||||||||||||||||||
|
归纳小结 |
课堂小结 解决应用用问题的步骤: 读题-列式-解答. |
学生总结,师生完善 |
使学生养成归纳总结的好习惯.让学生初步掌握数学建模的基本过程. |
|||||||||||||||||||||||||||||||
|
布置作业 |
习题2-3B第1、3题: 教材第71页“思考与讨论”. |
学生练习 |
使学生巩固本节所学知识与方法. |
备选例题
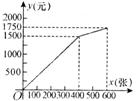 例1 某游艺场每天的盈利额y元与售出的门票数x张之间的关系如图所示,试问盈利额为750元时,当天售出的门票数为多少?
例1 某游艺场每天的盈利额y元与售出的门票数x张之间的关系如图所示,试问盈利额为750元时,当天售出的门票数为多少?
[解析]根据题意,每天的盈利额y元与售出的门票数x张之间的函数关系是:
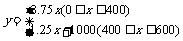
(1)当0≤x≤400时,由3.75x=750,得x=200.
(2)当400≤x≤600时,由1.25x + 1000 = 750,得x = – 200 (舍去).
综合(1)和(2),盈利额为750元时,当天售出的门票数为200张.
答:当天售出的门票数为200张时盈利额为750元.
例2 某个经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表:
|
投资A种商品金额(万元) |
1 |
2 |
3 |
4 |
5 |
6 |
|
获纯利润 (万元) |
0.65 |
1.39 |
1.85 |
2 |
1.84 |
1.40 |
|
投资B种商品金额(万元) |
1 |
2 |
3 |
4 |
5 |
6 |
|
获纯利润 (万元) |
0.25 |
0.49 |
0.76 |
1 |
1.26 |
1.51 |
该经营者准备下月投入12万元经营这两种产品,但不知投入A、B两种商品各多少才最合算. 请你帮助制定一个资金投入方案,使得该经营者获得最大的利润,并按你的方案求出该经营者下月可获得的最大纯利润(结果保留两位有效数字).
[解析]以投资额为横坐标,纯利润为纵坐标,在直角坐标系中画出散点图:
据此,可考虑用下列函数分别描述上述两组数据之间的对应关系.
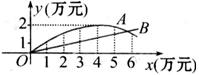 y = – a (x – 4)2 + 2 (a>0) ①
y = – a (x – 4)2 + 2 (a>0) ①
y = bx ②
把x = 1,y = 0.65代入①式,得
0.65 = – a (1 – 4)2 + 2,
解得a = 0.15.
故前六个月所获纯利润关于月投资A商品的金额的函数关系式可近似地用y = – 0.15(x – 4)2 + 2表示,再把x = 4,y = 1代入②式,得b = 0.25,故前六个月所获利润关于月投资B种商品的金额的函数关系可近似地用y = 0.25x表示.
设下月投资A种商品x万元,
则投资B种商品为(12 – x)万元,可获纯利润
y = – 0.15 (x – 4)2 + 2 + 0.25 (12 – x)
= – 0.15x2 + 0.95x + 2.6,
当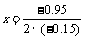 ≈3.2时,
≈3.2时,
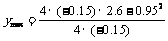 ≈4.1.
≈4.1.
故下月分别投资A、B两种商品3.2万元和8.8万元,可获最大纯利润4.1万元.
[评析]幂函数模型的应用题经常以二次函数的形式出现,要注意y = x2变换到y = a (x – m)2 + b后发生的变化.
本节内容主要是例题教学,因此采用学生探究解题方法,总结解题规律,教师启发诱导的方法进行教学.
一次和二次函数模型的应用是本节的重点,数学建模是本节的难点.
3.情感、态度与价值观:了解数学知识来源于生活,又服务于实际,从而培养学生的应用意识,提高学习数学的兴趣.
2.过程与方法:经历运用一次和二次函数模型解决实际问题,提高学生的数学建模能力.
1.知识与技能:初步掌握一次和二次函数模型的应用,会解决较简单的实际应用问题.
尝试指导与合作交流相结合,学生自主学习和老师引导相结合.解决实际问题范例,培养学生利用函数增长快慢的数学知识对实际问题进行探究和决策.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com