8．已知直线l₁：x+my+6＝0，l₂：(m－2)x+3y+2m＝0，求m的值，使得：

　 (1)l₁与l₂相交；(2)l₁⊥l₂；(3)l₁∥l₂；(4)l₁，l₂重合．

　 解答：(1)由已知1×3≠m(m－2)，即m²－2m－3≠0，

　 解得m≠－1且m≠3.故当m≠－1且m≠3时，l₁与l₂相交．

　 (2)当1·(m－2)+m·3＝0，即m＝时，l₁⊥l₂.

　 (3)当＝≠，即m＝－1时，l₁∥l₂.

　 (4)当＝＝，即m＝3时，l₁与l₂重合．

7．若经过点P(1－a,1+a)和Q(3,2a)的直线的倾斜角为锐角，则实数a的取值范围是________．

　 解析：由条件知直线的斜率存在，由公式得k＝，

　 因为倾斜角为锐角，所以k>0，解得a>1或a<－2

　 所以a的取值范围是{a|a>1或a<－2}．

　 答案：(－∞，－2)∪(1，+∞)

6．已知点A(－2,4)、B(4,2)，直线l过点P(0，－2)与线段AB相交，则直线l的斜率k的取值范围是________．

　 解析：数形结合法．由k_PA＝－3，k_PB＝1，

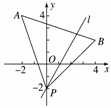
　 如图得直线l的斜率k的取值范围是(－∞，－3]∪[1，+∞)．

　 答案：k≥1或k≤－3

5．若过点P(1－a,1+a)和Q(3,2a)的直线的倾斜角α为钝角，则实数a的取值范围为 __________．

　 解析：k＝tan α＝<0，∴－2<a<1.

　 答案：(－2,1)

4．设直线l的方程为x+ycos θ+3＝0 (θ∈R)，则直线l的倾斜角α的范围是(　)

　 A．[0，π)　 　　　　 B.　

　 C.　 　　　　 D.∪

　 解析：当cos θ＝0时，方程变为x+3＝0，其倾斜角为；

　 当cos θ≠0时，由直线方程可得斜率k＝－.

　 ∵cos θ∈[－1,1]且cos θ≠0，∴k∈(－∞，－1]∪[1，+∞)，

　 即tan α∈(－∞，－1]∪[1，+∞)，又α∈[0，π)，∴α∈∪.

　 由上知，倾斜角的范围是，故选C.

　 答案：C

3．直线l₁：ax+by+c＝0，直线l₂：mx+ny+d＝0，则＝－1是直线l₁⊥l₂的(　)

　 A．充要条件　 　　　　　　　　　　　 B．既不充分也不必要条件

　 C．必要不充分条件　 　　　 D．充分不必要条件

　 答案：D

2．下列四个命题：

　 ①一条直线向上的方向与x轴正向所成的角，叫做这条直线的倾斜角；

　 ②直线l的倾斜角的取值范围是第一象限角或第二象限角；

　 ③已知直线l经过P₁(x₁，y₁)，P₂(x₂，y₂)两点，则直线l的斜率k＝；

　 ④与x轴垂直的直线斜率为0.

　 其中正确命题的个数是(　)

　 A．3个　 B．2个　 C．1个　 D．0个

　 答案：D

1．若直线l沿x轴负方向平移3个单位，再沿y轴正方向平移1个单位后，又回到原来位置，那么直线l的斜率是(　)

　 A．－　 B．－3　 C.　 D．3

　 解析：设P(a，b)为l上任一点，经过如上平移后，点P到达点Q(a－3，b+1)，

　 此时直线PQ与l重合．故l的斜率k＝k_PQ＝＝－.

　 答案：A

29．(8分)读图15“我国西部雪线高度分布图”，回答下列问题。

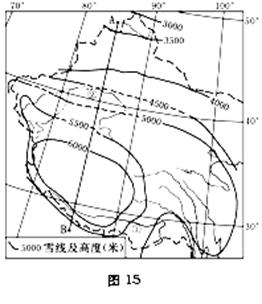
(1)沿图中AB线雪线高度的变化规律是什么？(2分)

(2)河流①流域内的种植业主要集中在河谷地区，试分析其形成原因。(2分)

(3)河流②流域内种植业区存在的主要生态环境问题是什么？有何相应的防治措施？(4分)