
1.练习:课本第78页 练习:4;习题:*6⑴,*7⑴.
答案:7⑴∵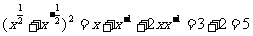 ,
,
∴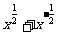 =
=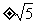 ,又由已知
,又由已知 得x>0,于是
得x>0,于是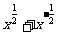 >0,
>0,
∴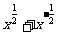 =
= .
.
例1.用分数指数幂表示下列分式(其中各式字母均为正数)
(1) (2)
(2)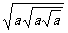 (3)
(3)
(4)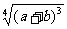 (5)
(5) (6)
(6)
解:(1)
(2) 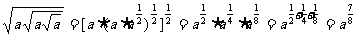
(3) 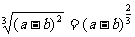
(4)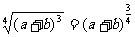
(5)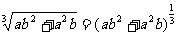
(6)
例2(课本第77页 例4)计算下列各式(式中字母都是正数):
⑴ 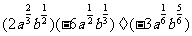 ;⑵
;⑵
 .
.
解:⑴原式=[2×(-6)÷(-3)] ;
;
⑵原式=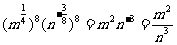
说明:该例是运用分数指数幂的定义和运算性质进行计算的题,第⑴小题是仿照单项式乘除法进行的,首先将系数相乘除,然后将同底数的幂相乘除;第⑵小题是先按积的乘方计算,再按幂的乘方计算,在计算过程中要特别注意符号. 同学们在下面做题中,刚开始时,要严格按照象例题一样的解题步骤进行,待熟练以后再简化计算步骤.
例3(课本第77页 例5) 计算下列各式:
⑴  ;⑵
;⑵
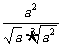 (a>0).
(a>0).
解:⑴原式=
= ;
;
⑵原式=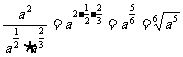 .
.
说明:本例是利用分数指数幂来进行根式计算,其顺序是先把根式化为分数指数幂,再根据幂的运算性质进行计算;对于计算结果,若没有特别要求,就用分数指数幂的形式表示,若有特殊要求,可根据要求给出结果,但结果不能同时含有根号和分数指数,也不能既有分母又含有负指数
例4化简:
解:

评述:此题注重了分子、分母指数间的联系,即 ,由此联想到平方差公式的特点,进而使问题得到解决
,由此联想到平方差公式的特点,进而使问题得到解决
例5 已知x+x-1=3,求下列各式的值:

分析:(1)题若平方则可出现已知形式,但开方时应注意正负的讨论;
(2)题若立方则可出现(1)题形式与已知条件,需将已知条件与(1)题结论综合;或者,可仿照(1)题作平方处理,进而利用立方和公式展开
解:
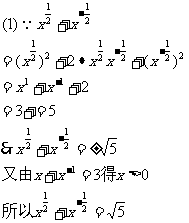

评述:(1)题注重了已知条件与所求之间的内在联系,但开方时正负的取舍容易被学生所忽视,应强调以引起学生注意
(2)题解法一注意了(1)题结论的应用,显得颇为简捷,解法二注重的是与已知条件的联系,体现了对立方和公式、平方和公式的灵活运用,耐用具有一定层次,需看透问题实质方可解决得彻底,否则可能关途而废另外,(2)题也体现了一题多解
2.分数指数幂的运算性质:

1.根式的运算性质:
①当n为任意正整数时,(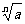 )
)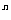 =a.
=a.
②当n为奇数时,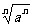 =a;当n为偶数时,
=a;当n为偶数时,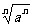 =|a|=
=|a|= .
.
⑶根式的基本性质: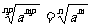 ,(a
,(a 0).
0).
22.(14分)
在 中,角A、B、C所对的边分别为a,b,c,已知
中,角A、B、C所对的边分别为a,b,c,已知
(I)求 的值;
的值;
(II)当a=2, 时,求b及c的长.
时,求b及c的长.
21.(12分)
在△ABC中,已知(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,试确定△ABC的形状。
20.(12分)
设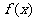 满足
满足 求
求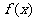 的表达式.
的表达式.
19.(12分)
已知函数
(1)求它的定义域、值域以及在什么区间上是增函数;
(2)判断它的奇偶性;
(3)判断它的周期性。
18.(12分)
已知sinθ+2cosθ=0,求 的值。
的值。
17.(12分)
求值: 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com