
6.设mn>0,x=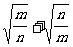 ,化简:A=
,化简:A=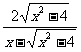 .
.
解:∵x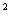 -4=(
-4=(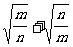 )
)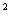 -4=(
-4=(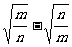 )
)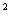 ,
,
∴A=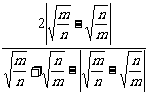 =
=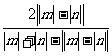 ,
,
又∵mn>0,∴m,n同号.
⑴设m>0,且n>0,则A=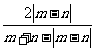 .
.
①若m n,则A=
n,则A=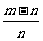 ;②若m<n,则A=
;②若m<n,则A=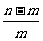 .
.
⑵设m<0,且n<0,则A=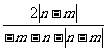 .
.
①若n m,则A=
m,则A=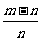 ;②若n<m,则A=
;②若n<m,则A=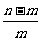 .
.
综上所述得:A=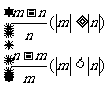 .
.
5.求值: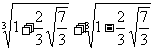 .
.
解:设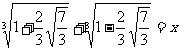 ,由公式
,由公式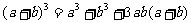 得
得
(1+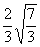 )+(1-
)+(1-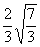 )+3
)+3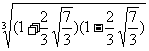 x=x3,即x3+x-2=0,
x=x3,即x3+x-2=0,
分解因式得: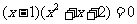 ,
,
∵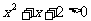 ,∴
,∴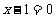 ,即x=1,∴原式=1.
,即x=1,∴原式=1.
4.已知: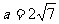 ,
,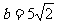 ,求
,求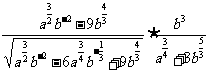 的值.
的值.
解:由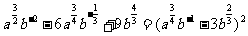 ,
,
又1<a<b,∴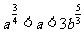 ,从而得
,从而得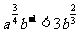 ,
,
∴原式=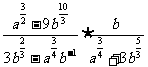 =
=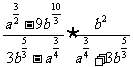
=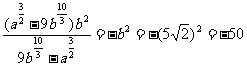 .
.
3.已知: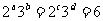 ,求证:
,求证: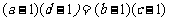 .
.
证明:由已知得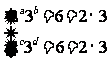
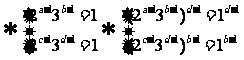

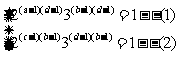 ,
,
⑴÷⑵,得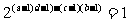 ,
,
∴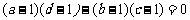 ,即
,即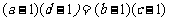
7.⑵ ∵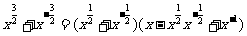 ,
,
而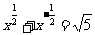 (由⑴知),
(由⑴知), ,
,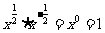 ,
,
∴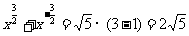 ;
;
⑶ ∵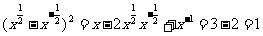 ,∴
,∴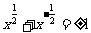 ;
;
⑷ 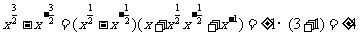 .
.
2.课本第75页 习题2.5:6 ⑵,7 ⑵⑶⑷.
解:6.⑵ 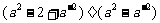 =
=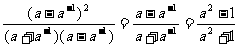 ;
;
1.求下列各式的值:
(1) (2)
(2)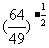 (3)
(3)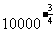 (4)
(4)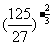
解:(1)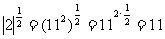
(2)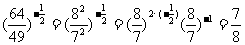
(3) 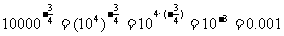
(4) 
熟练进行有关分数指数幂是计算,熟练掌握分数指数幂的定义和运算性质
2. 练习求下列各式的值:
(1)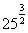 (2)
(2)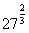 (3)
(3)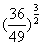
(4)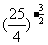 (5)
(5)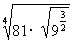 (6)
(6)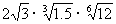
解:(1) 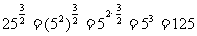
(2) 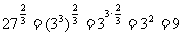
(3)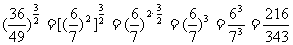
(4) 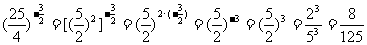
(5) 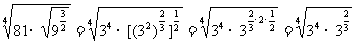
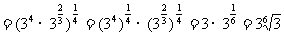
(6) 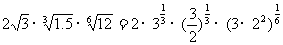
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com