
1.设集合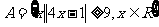 ,
, 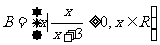 , 则A∩B= ( )
, 则A∩B= ( )
A.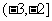 B.
B.
C.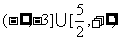 D.
D.
22.解:(1)由题意知,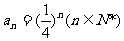
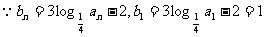
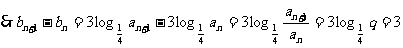
∴数列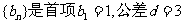 的等差数列.
的等差数列.
(2)由(1)知,
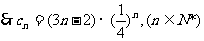

于是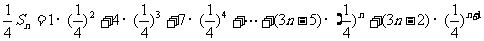
两式相减得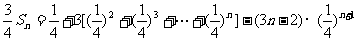
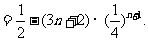
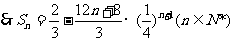
(3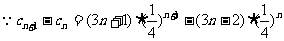
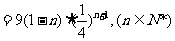
∴当n=1时,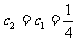
当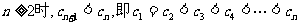 ∴当n=1时,
∴当n=1时,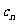 取最大值是
取最大值是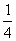
又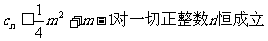
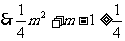
即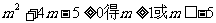 .
.
.
21. 解:(1) 在x∈
在x∈ 时恒成立.即
时恒成立.即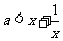 在x∈
在x∈ 时恒成立.
时恒成立.
又函数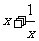 在
在 上是增函数,所以
上是增函数,所以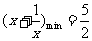 ,从而
,从而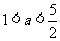 .----------------6分
.----------------6分
(2)A=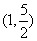 ,B=
,B=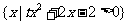 .
.
由于A∩B≠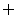 ,所以不等式
,所以不等式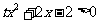 有属于A的解,
有属于A的解,
即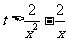 有属于A的解.-------------------------------------------8分
有属于A的解.-------------------------------------------8分
又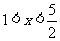 时,
时,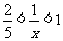 ,所以
,所以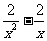 =
=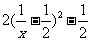 ∈
∈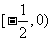 .故
.故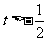 .-----12分
.-----12分
20. 解:(1)∵方程ax2+bx-2x=0有等根,∴△=(b-2)2=0,得b=2.
由f(x-1)=f(3-x)知此函数图像的对称轴方程为x=-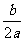 =1,
=1,
得a=-1,
故f(x)=-x2+2x.
(2)∵f(x)=-(x-1)2+1≤1,∴4n≤1,即n≤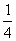 .
.
而抛物线y=-x2+2x的对称轴为x=1,
∴当n≤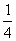 时,f(x)在[m,n]上为增函数.
时,f(x)在[m,n]上为增函数.
若满足题设条件的m,n存在,则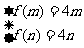
即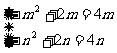

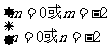
 又m<n≤
又m<n≤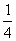 .
.
∴m=-2,n=0,
这时,定义域为[-2,0],值域为[-8,0].
由以上知满足条件的m,n存在,m=-2,n=0.
22. (本题12分)
已知数列 ,设
,设
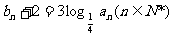 ,数列
,数列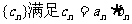 。
。
(1)求证: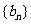 是等差数列;
是等差数列;
(2)求数列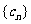 的前n项和
的前n项和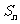 ;
;
(3)若 一切正整数n恒成立,求实数m取值范围
一切正整数n恒成立,求实数m取值范围 19(Ⅰ)解:
19(Ⅰ)解: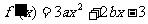 ,依题意,
,依题意, ,即
,即
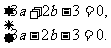 解得
解得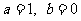 .-----------------3分
.-----------------3分
∴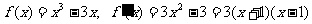 .
.
令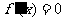 ,得
,得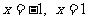 .
.
若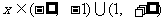 ,则
,则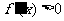 ,
,
故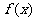 在
在 上是增函数,
上是增函数,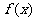 在
在 上是增函数.
上是增函数.
若 ,则
,则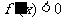 ,故
,故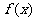 在
在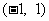 上是减函数.
上是减函数.
所以,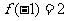 是极大值;
是极大值;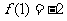 是极小值.------------------6分
是极小值.------------------6分
(Ⅱ)解:曲线方程为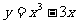 ,点
,点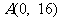 不在曲线上.
不在曲线上.
设切点为 ,则点M的坐标满足
,则点M的坐标满足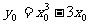 .
.
因 ,故切线的方程为
,故切线的方程为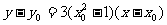 ---------8分
---------8分
注意到点A(0,16)在切线上,有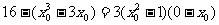
化简得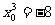 ,解得
,解得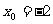 .------------------------------------10分
.------------------------------------10分
所以,切点为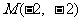 ,切线方程为
,切线方程为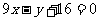 .---------------12分
.---------------12分
由于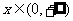 ,于是
,于是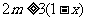 ,得
,得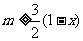 ,而
,而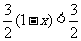 ,所以
,所以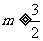 .
.
21.(本题12分)
已知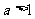 , 函数
, 函数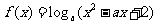 在x∈
在x∈ 时的值恒为正.
时的值恒为正.
(1)a的取值范围;
(2)记(1)中a的取值范围为集合A, 函数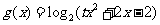 的定义域为集合B.若A∩B≠
的定义域为集合B.若A∩B≠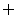 , 求实数t的取值范围.
, 求实数t的取值范围.
20. (本题12分)
已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件f(x-1)=f(3-x)且方程f(x)=2x有等根.
(1)求f(x)的解析式;
(2)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],如果存在,求出m,n的值;如果不存在,说明理由.
19、(本题12分)
已知函数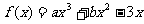 在
在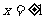 处取得极值.
处取得极值.
(Ⅰ)讨论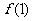 和
和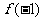 是函数
是函数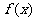 的极大值还是极小值;
的极大值还是极小值;
(Ⅱ)过点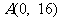 作曲线
作曲线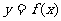 的切线,求此切线方程.
的切线,求此切线方程.
18.(本题12分)已知a>0且a≠1,设p:函数y=ax在R上单调递增,q:设函数y=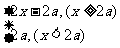 ,函数y≥1恒成立,若p∧q为假,p∨q为真,求实数a的取值范围.
,函数y≥1恒成立,若p∧q为假,p∨q为真,求实数a的取值范围.
17.(本题10分)
记函数 的定义域为集合A,函数
的定义域为集合A,函数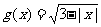 的定义域为集合B.
的定义域为集合B.
(1)求A∩B和A∪B;
(2)若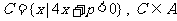 ,求实数
,求实数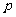 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com