
5、从卫星云图上能清晰看到台风的中心位置及移动方向,其卫星云图的获取来自 ( )
A、RS技术 B、GIS技术 C、GPS技术 D、观测资料
 图1是我国东部某山地地形剖面图及自然带垂直分布图,读后完成3--4题:
图1是我国东部某山地地形剖面图及自然带垂直分布图,读后完成3--4题:
3、该山地位于 ( )
A、华南热带湿润地区
B、华中亚热带湿润地区
C、华北暖温带湿润、半湿润地区
D、东北温带湿润、半湿润地区
4、决定该山山麓自然带分布的主导因素是( )
A、海陆位置 B、纬度位置
C、山脉走向 D、山体坡度
2、下列地理事物由大到小或由强到弱排列的是 ( )
A、 区位优势:东部、中部、西部 B、作物熟制:东北、华中、华南
C、面积:东部、中部、西部 D、GDP的增长:西部、中部、东部
1、流经三大自然区,流域跨三个经济地带的河流是 ( )
A、长江 B、黄河 C、海河 D、珠江
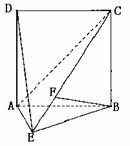
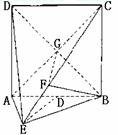
10.( 2005福建)如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离.
分析:本小题主要考查直线、直线与平面、二面角及点到平面的距离等基础知识,考查空间想象能力,逻辑思维能力与运算能力.
解法一:
(Ⅰ)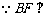 平面ACE.
平面ACE. 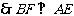 .
.
∵二面角D-AB-E为直二面角,且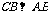 ,
, 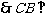 平面ABE.
平面ABE.
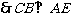
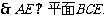
(Ⅱ)连结BD交AC于C,连结FG,
∵正方形ABCD边长为2,
∴BG⊥AC,BG=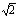 ,
,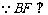 平面ACE,
平面ACE,
由三垂线定理的逆定理得FG⊥AC.
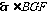 是二面角B-AC-E的平面角.
是二面角B-AC-E的平面角.
由(Ⅰ)AE⊥平面BCE, 又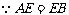 ,
,
∴在等腰直角三角形AEB中,BE=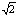 .
.
又 直角
直角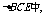

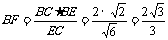 ,
,
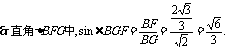
∴二面角B-AC-E等于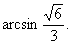
(Ⅲ)过点E作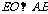 交AB于点O. OE=1.
交AB于点O. OE=1.
∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,
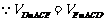
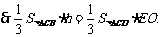
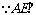 平面BCE,
平面BCE,
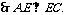
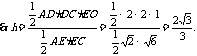
∴点D到平面ACE的距离为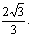
9.(2004天津) 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(Ⅰ)证明PA//平面EDB;
(Ⅱ)证明PB⊥平面EFD;
(Ⅲ)求二面角C-PB-D的大小.

(1)证明:连结AC,AC交BD于O,连结EO.
∵底面ABCD是正方形,
∴点O是AC的中点
在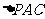 中,EO是中位线,∴PA // EO
中,EO是中位线,∴PA // EO
而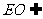 平面EDB且
平面EDB且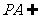 平面EDB,
平面EDB,
所以,PA // 平面EDB
(2)证明:∵PD⊥底面ABCD且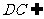 底面ABCD,
底面ABCD,
∴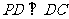 ∵PD=DC,可知
∵PD=DC,可知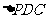 是等腰直角三角形,而DE是斜边PC的中线,
是等腰直角三角形,而DE是斜边PC的中线,
∴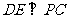 .
①
.
①
同样由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,
∴BC⊥平面PDC.
而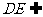 平面PDC,∴
平面PDC,∴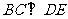 . ②
. ②
由①和②推得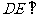 平面PBC.
平面PBC.
而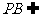 平面PBC,∴
平面PBC,∴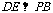
又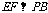 且
且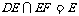 ,
,
所以PB⊥平面EFD.
(3)解:由(2)知,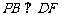 ,故
,故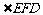 是二面角C-PB-D的平面角.
是二面角C-PB-D的平面角.
由(2)知,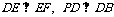 .
.
设正方形ABCD的边长为a,则
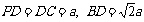 ,
,
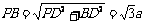 ,
,
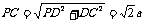 ,
,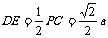 .
.
在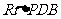 中,
中,
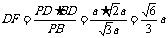 .
.
在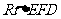 中,
中,
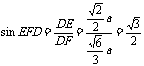 ,
,
∴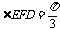 ,二面角C-PB-D的大小为
,二面角C-PB-D的大小为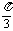 .
.
8.已知矩形ABCD中,AB=1, BC=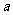 (
(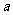 >0),PA⊥面ABCD,PA=1
>0),PA⊥面ABCD,PA=1
(1)问BC边上是否存在一点Q,使得PQ⊥QD并且说明理由
(2)若BC边上有且只有一个点Q使得PQ⊥QD,求这时二面角Q-PD-A大小


解:(1) a=2时只有一点;a>2时有两点;a<2时没有点;
 (2)arctan
(2)arctan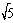
7.在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90ο ,E为C1C的中点 ,F
是BB1上是BF=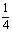 BB1,AC=AA1=2
BB1,AC=AA1=2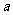 ,求平面EFA与面ABC所成角的大小
,求平面EFA与面ABC所成角的大小
答案: arctan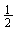
5. 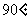 ;
6.[0°,90°];
;
6.[0°,90°];
提示:3. l⊥平面PAB于C,PC是ΔPAB外接圆直径,用余、正弦定理.
[解答题]
6.一条直线与直二面角的两个面所成的角分别是α和β,则α+β的范围是_____.
◆答案提示: 1-3. BCB; 4. a⊥b;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com