
3.情感、态度与价值观
在学习过程中,学会整合知识,提升自我学习的品质,养成合作、交流、创新的良好学习品质.
2.过程与方法
通过学生自我回顾、反思、整理、归纳所学知识,从而构建本节的知识体系.
1.知识与技能.
整合函数模型及其应用的基本知识与基本方法. 进一步提升研究函数和应用函数解决实际应用问题的技能.
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
回顾反思构建体系 |
1.函数与方程单元知识网络    2.知识梳理  ①二次函数的零点与一元二次方程根的关系  对于二次函数f (x) = ax2 + bx + c (a≠0),当f (x) = 0时,就是一元二次方程ax2 + bx + c = 0,因此,二次函数f (x) = ax2 + bx + c (a≠0)的零点就是一元二次方程ax2 + bx + c = 0的根;也即二次函数f (x) = ax2 + bx + c的图象--抛物线与x轴相交时,交点的横坐标就是一元二次方程ax2 + bx + c = 0的根.  ②函数的零点的理解  (1)函数的零点是一个实数,当自变量取该值时,其函数值等于零.  (2)根据函数零点定义可知,函数f (x)的零点就是f (x) = 0的根,因此判断一个函数是否有零点,有几个零点,就是判断方程f (x) = 0是否有实根,有几个实根.  ③函数零点的判定  判断一个函数是否有零点,首先看函数f (x)在区间[a,b]上的图象是否连续,并且是否存在f (a)·f (b)<0,若满足,那么函数y = f (x)在区间(a,b)内必有零点.  ④用二分法求方程的近似解要注意以下问题:  (1)要看清题目要求的精确度,它决定着二分法步骤的结束.  (2)初始区间的选定一般在两个整数间,不同的初始区间结果是相同的,但二分的次数却相差较大.  (3)在二分法的第四步,由|a – b|< 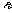 ,便可判断零点近似值为a或b. ,便可判断零点近似值为a或b. ⑤用二分法求曲线的近似交点应注意以下几点:  (1)曲线的交点坐标是方程组的解,最终转化为求方程的根;  (2)求曲线y = f (x)和y = g(x)的交点的横坐标,实际上就是求函数y = f (x) – g (x)的零点,即求方程f (x) – g (x) = 0的实数解. |
1.师生合作,绘制单元知识网络图 2.学生回顾口述知识要点,老师总结、归纳,师生共同进行知识疏理. |
整理知识,培养归纳能力;师生共同回顾、再现知识与方法. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
经典例题剖析 |
 例1 利用计算器,求方程2x + 2x – 5 = 0的近似解. (精确到0.1)         例2 确定函数f (x) = 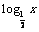 + x
– 4 的零点个数. + x
– 4 的零点个数.      例3(1)试说明方程2x3 – 6x2 +3 = 0有3个实数解,并求出全部解的和(精确到0.01)  (2)探究方程2x3 – 6x2 +5 = 0,方程2x3 – 6x2 +8 = 0全部解的和,你由此可以得到什么结论?  |
1.学生自主完成例1、例2、例3,求解学生代表板书解答过程,老师点评,总结. 例1[解析]设f (x) = 2x + 2x – 5,由于函数在R上是增函数,所以函数f (x)在R上至多一个零点. ∵f (1) = –1<0,f (2) = 3>0, ∴f (1) f (2)<0, ∴函数f (x) = 2x + 2x – 5在(1, 2)内有一个零点,则二分法逐次计算,列表如下:
∵|1.3125 – 1.25| = 0.0625<0.1, ∴函数f (x)的零点近似值为1.3125. ∴方程2x + 2x – 5 = 0的近似解是1.3125. 例2[解析]设,则f (x)的零点个数即y1与y2的交点个数,作出两函数图象如图.
由图知,y1与y2在区间(0, 1)内有一个交点, 当x = 4时,y1 = –2,y2 = 0, 当x = 8时,y1 = –3,y2 = – 4, ∴在(4, 8)内两曲线又有一个交点,又 ∴两曲线只有两个交点, 即函数 例3[解析](1)设函数 f (x) =2x3 – 6x2 +3, ∵f (–1) = –5<0,f (0) = 3>0,f (1) = –1<0, f (2) = –5<0,f (3) = 3>0,函数y = f (x)的图象是连续的曲线,∴方程2x3 – 6x2 +3 = 0有3个实数解. 首先以区间[–1,0]为计算的初始区间,用二分法逐步计算,列表如下:
由上表计算可知,区间[– 0.64453125,– 0.640625]的左、右两端点精确到0.01所取的近似值都是 – 0.64,所以– 0.64可以作为方程2x3 – 6x2 +3 = 0在区间[–1,0]上的一个近似解. 同理可求得方程2x3 – 6x2 +3 = 0在区间[0,1]和[2,3]内且精确到0.01的近似解分别为0.83,2.81.所以方程2x3 – 6x2 +3 = 0全部解的和为– 0.64 + 0.83 + 2.81 = 3. (2)利用同样方法可求得方程2x3 – 6x2 +5 = 0和方程2x3 – 6x2 +8 = 0全部解的和也为3. 由于3只与未知数的系数比相等,即 – (– 6÷2) = 3,所以猜想: 一般地,对于一元三次方程ax3+ bx3 + cx +d = 0有三个根xl,x2,x3,则和为x1 +x2
+x3 = |
动手尝试练习提升综合应用知识的能力. |
备选例题
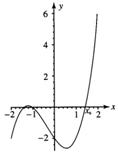
例1 求函数y = x3 – 2x2 – x + 2的零点,并画出它的图象.
[解析]因为x3 – 2x – x + 2 = x2 (x – 2) – (x – 2) = (x – 2) (x2 – 1) = (x – 2) (x – 1) (x + 1),
所以已知函数的零点为–1,1,2.
3个零点把x轴分成4个区间:
 ,[–1,1],[1,2],
,[–1,1],[1,2],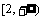 .
.
在这4个区间内,取x的一些值(包括零点),列出这个函数的对应值表:
|
x |
… |
–1.5 |
–1 |
–0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
… |
|
y |
… |
–
4.38 |
0 |
1.88 |
2 |
1.13 |
0 |
–0.63 |
0 |
2.63 |
… |
在直角坐标系内描点连线,这个函数的图象如图所示.
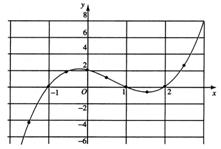
例2 求函数f (x) = x3 + x2 – 2x – 2的一个为正实数的零点(误差不超过0.1).
[解析]由于f (1) = –2<0,f (2) = 6>0,可以取区间[1,2]作为计算的初始区间.
用二分法逐次计算,列表如下:
|
端点(中点)坐标 |
计算中点的函数值 |
取区间 |
|an – bn| |
|
|
|
[1,2] |
1 |
|
x0 = (1 + 2)/2 = 1.5 |
f(x0)=0.625>0 |
[1,1.5] |
0.5 |
|
x1 = (1 + 1.5)/2 = 1.25 |
f(x1)= –0.984<0 |
[1.25,1.5] |
0.25 |
|
x2=(1.25+1.5)/2 =1.375 |
f(x2)= –0.260<0 |
[1.375,1.5] |
0.125 |
|
x3=(1.375+1.5)/2=1.438 |
|
|
|
 由上表的计算可知,区间[1.375,1.5 ]的长度小于0.2,所以这个区间的中点x3 =
1.438可作为所求函数误差不超过0.1的一个正实数零点的近似值.
由上表的计算可知,区间[1.375,1.5 ]的长度小于0.2,所以这个区间的中点x3 =
1.438可作为所求函数误差不超过0.1的一个正实数零点的近似值.
函数f (x) = x3 + x2 – 2x – 2的图象如图所示.
实际上还可用二分法继续算下去,进而得到这个零点精确度更高的近似值.
动手练习与合作交流相结合,在整合知识中构建单元知识体系,在综合练习中提升综合运用单元知识的能力.
重点:整合单元知识;难点:提升综合运用单元知识的能力.
3.情感、态度与价值观
在学习过程中,学会整合知识,提升自我学习的品质,养成合作、交流、创新的良好学习品质.
2.过程与方法
通过学生自我回顾、反思、整理、归纳所学知识,从而构建本节的知识体系
1.知识与技能
整合函数与方程的基本知识和基本方法,进一步提升函数与方程思想.
15.(20分)在光滑的水平面上停放着一辆质量为m1的小车,小车上放置一个质量为m2的物块,现将轻弹簧压缩在物块与小车左边固定挡板之间,并用细线拴住,使m2静止在小车上的A点,如图所示。设物块与小车之间的动摩擦因数为μ,O点为弹簧原长的位置,将细线烧断后,m2 、m1开始运动。
(1)问m2 位于O点左侧还是右侧时,物体m2 的速度最大?
 (2)若物体m2 达最大速度
(2)若物体m2 达最大速度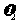 时,物体m2 已相对小车移动了距离s,求此时m1的速度
时,物体m2 已相对小车移动了距离s,求此时m1的速度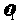 和这一个过程弹簧释放的弹性势能;
和这一个过程弹簧释放的弹性势能;
(3)如果在细线烧断前弹簧的弹性势能为E,A点到小车最右端的距离为L,则当E满足什么条件物块m2能离开小车,并求离开小车时物块的速度
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com