
2.我国三大自然区域间的差异从地形地势、气候、植被土壤、水文及人类活动等方面进行比较分析,从而突显其知识要点(见右表)。
难点分析
三大自然区的划分涉及到“区域”和“界线”两大难点问题。
1.地形、气温和降水这三个要素是划分三大自然区的主要参考依据。
18.解:(1)设前n个月投资总额为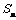 ,
,
则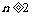 时,
时, ,∴
,∴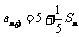 ,
,
两式相减得: ,∴
,∴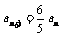 ,
,
又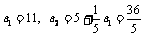 ,∴
,∴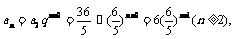
又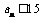 ,∴
,∴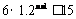 ,∴
,∴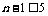 ,∴
,∴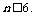
∴
(2)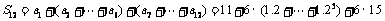
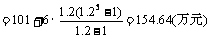
故预计2010年全年共需投资154.64万元.
21.(本题满分12分)某企业为了适应市场需求,计划从2010年元月起,在每月固定投资5万元的基础上,元月份追加投资6万元,以后每月的追加投资额均为之前几个月投资额总和的20%,但每月追加部分最高限额为10万元. 记第n个月的投资额为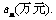
(1)求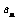 与n的关系式;
与n的关系式;
(2)预计2010年全年共需投资多少万元?(精确到0.01,参考数据: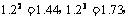
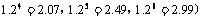
17.解:(1)由题设知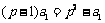 ,解得
,解得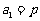 。
。
由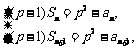 两式作差得
两式作差得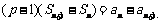
所以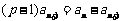 ,即
,即 ,
,
可见,数列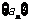 是首项为
是首项为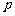 ,公比为
,公比为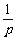 的等比数列。
的等比数列。
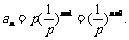
(2)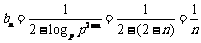 .
.
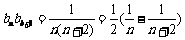
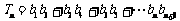
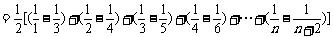
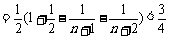 。
。
20.(本题满分12分)已知数列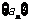 的各项均是正数,其前
的各项均是正数,其前 项和为
项和为 ,满足
,满足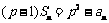 ,其中
,其中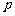 为正常数,且
为正常数,且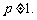
(1)求数列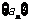 的通项公式;
的通项公式;
(2)设 ,数列
,数列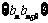 的前
的前 项和为
项和为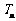 ,求证:
,求证: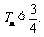
16.解:(1)依题意,得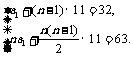 解得:
解得: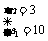
(2) 解得:
解得: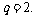
从而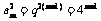 ,∴
,∴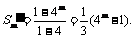
19.(本小题满分12分)数列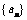 中,
中,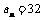 ,
,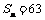 ,
,
(1)若数列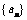 为公差为11的等差数列,求
为公差为11的等差数列,求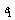 ;
;
(2)若数列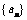 为以
为以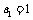 为首项的等比数列,求数列
为首项的等比数列,求数列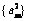 的前m项和
的前m项和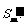
18.(本小题满分14分)
已知数列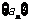 的前n项和为
的前n项和为 ,且
,且
(1)求数列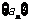 的通项公式;
的通项公式;
(2)设数列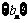 满足:
满足: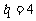 ,且
,且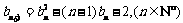 ,
,
求证: ;
;
(3)求证: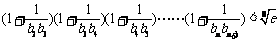 。
。
解:(1)当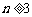 时,
时,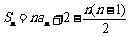 ,
,
 ,可得:
,可得: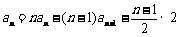 ,
,
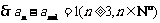 .
.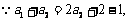
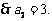
可得,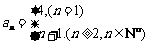
(2)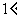 当
当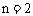 时,
时,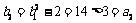 ,不等式成立.
,不等式成立.
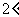 假设当
假设当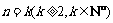 时,不等式成立,即
时,不等式成立,即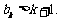 那么,当
那么,当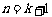 时,
时,
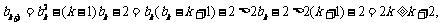
所以当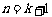 时,不等式也成立。
时,不等式也成立。
根据(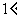 ),(
),(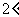 )可知,当
)可知,当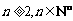 时,
时,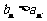
(3)设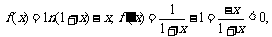
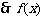 在
在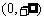 上单调递减,
上单调递减,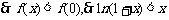
∵当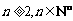 时,
时,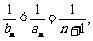
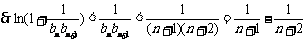 ,
,
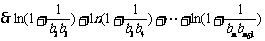
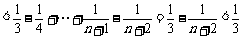
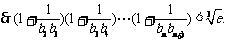
20.解析:(1)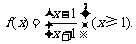
∵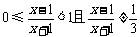 ,∴函数
,∴函数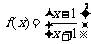 的值域为
的值域为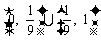
由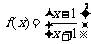 ,得
,得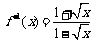 ,因此,函数
,因此,函数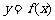 的反函数
的反函数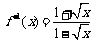
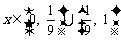
(2)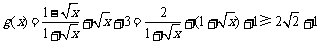 ,当且仅当
,当且仅当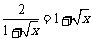 ,
,
即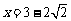 时,
时,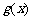 有最小值
有最小值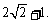
(3)由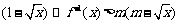 ,得
,得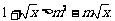
设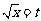 ,则
,则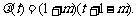
根据题意,对区间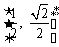 中的一切t值,
中的一切t值, 恒成立.
恒成立.
则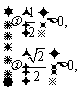 得
得 ∴
∴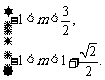
∴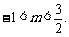 即实数m的取值范围是
即实数m的取值范围是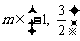
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com