
6.(2005湖北)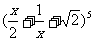 的展开式中整理后的常数项为
.
的展开式中整理后的常数项为
.
5.(2005辽宁)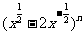 的展开式中常数项是
.
的展开式中常数项是
.
4.(2006浙江)若多项式
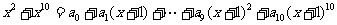 ,则a9等于 ( )
,则a9等于 ( )
(A)9 (B)10 (C)-9 (D)-10
3.(2006山东)已知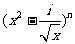 的展开式中第三项与第五项的系数之比为
的展开式中第三项与第五项的系数之比为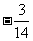 ,其中
,其中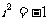 ,则展开式中常数项是 ( )
,则展开式中常数项是 ( )
A.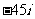 B.
B.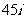 C.
C.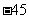 D.
D.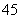
1.(2006重庆)若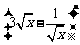 的展开式中各项系数之和为64,则展开式的常数项为 ( )
的展开式中各项系数之和为64,则展开式的常数项为 ( )
A.-540 B.-162 C.162 D.540
2已知(1-3x)9=a0+a1x+a2x2+…+a9x9,则|a0|+|a1|+|a2|+…+|a9|等于( )
A.29 B.49 C.39 D.1
3.二项式定理应用:
(1)求常数项、有理项和系数最大等特定的项;
(2)求和,证整除性;
(3)近似计算,(1+a)n≈1+na, (当|a|非常小时);
(4)二项式定理给出了一种计算方法,要注意在其它数学问题,如函数、数列、不等式中的应用。
2.二项式系数的性质:
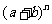 展开式的二项式系数是
展开式的二项式系数是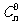 ,
,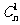 ,
,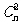 ,…,
,…,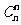 ,注意和系数的区别.
,注意和系数的区别.
(1)对称性.与首末两端“等距离”的两个二项式系数相等(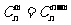 ).
).
直线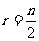 是图象的对称轴.
是图象的对称轴.
(2)增减性与最大值:当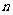 是偶数时,中间一项
是偶数时,中间一项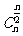 取得最大值;当
取得最大值;当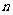 是奇数时,中间两项
是奇数时,中间两项 ,
,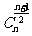 取得最大值。
取得最大值。
(3)各二项式系数和:由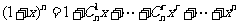 ,
,
令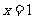 ,得
,得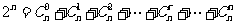
令x=-1,得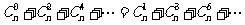
1.二项式定理: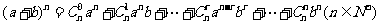 ,
,
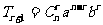
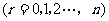 叫展开式的通项,是第r+1项.
叫展开式的通项,是第r+1项.
特例: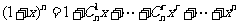
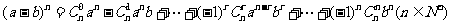
4.熟练掌握二项式定理的基本问题――通项公式及其应用
3.掌握二项式定理在近似计算及证明整除性中的应用
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com