
3.注意二项式定理在近似计算及证明整除性中的应用.
2.注意区分项的系数与项的二项式系数.
1.正确理解二项式定理,准确地写出二项式的展开式.
[例1]求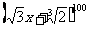 展开所得
展开所得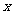 的多项式中,系数为有理数的项数
的多项式中,系数为有理数的项数
解: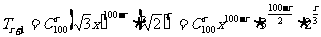
依题意: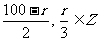 ,
,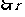 为3和2的倍数,即为6的倍数,
为3和2的倍数,即为6的倍数,
又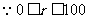 ,
,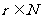 ,
,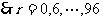 ,构成首项为0,公差为6,末项为96的等差数列,由
,构成首项为0,公差为6,末项为96的等差数列,由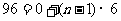 得
得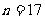 ,
,
故系数为有理数的项共有17项
◆提炼方法:有理项的求法:解不定方程,注意整除性的解法特征
[例2]设an=1+q+q2+…+q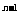 (n∈N*,q≠±1),An=C
(n∈N*,q≠±1),An=C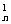 a1+C
a1+C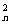 a2+…+C
a2+…+C an
an
(1)用q和n表示An;
(2)当-3<q<1时,求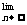
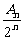

解:(1)因为q≠1,所以an=1+q+q2+…+q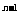 =
=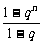

于是An= C
C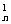 +
+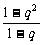 C
C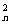 +…+
+…+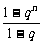 C
C
= [(C
[(C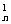 +C
+C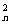 +…+C
+…+C )-(C
)-(C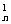 q+C
q+C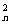 q2+…+C
q2+…+C qn)]
qn)]
= {(2n-1)-[(1+q)n-1]}
{(2n-1)-[(1+q)n-1]}
= [2n-(1+q)n]
[2n-(1+q)n]
(2)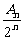 =
= [1-(
[1-(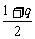 )n]
)n]
因为-3<q<1,且q≠-1,所以0<|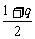 |<1
|<1
所以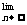
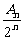 =
=

[例3]在二项式(axm+bxn)12(a>0,b>0,m、n≠0)中有2m+n=0,如果它的展开式里最大系数项恰是常数项.
(1)求它是第几项;(2)求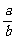 的范围.
的范围.
解:(1)设T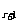 =C
=C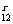 (axm)12-r·(bxn)r=C
(axm)12-r·(bxn)r=C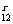 a12-rbrxm(12-r)+nr为常数项,则有m(12-r)+nr=0,即m(12-r)-2mr=0,∴r=4,它是第5项.
a12-rbrxm(12-r)+nr为常数项,则有m(12-r)+nr=0,即m(12-r)-2mr=0,∴r=4,它是第5项.
(2)∵第5项又是系数最大的项,
|
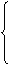 C
C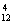 a8b4≥C
a8b4≥C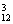 a9b3,
①
a9b3,
①
C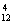 a8b4≥C
a8b4≥C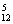 a7b5. ②
a7b5. ②
由①得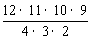 a8b4≥
a8b4≥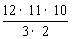 a9b3,
a9b3,
∵a>0,b>0,∴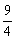 b≥a,即
b≥a,即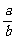 ≤
≤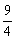 .
.
由②得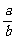 ≥
≥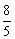 ,∴
,∴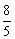 ≤
≤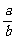 ≤
≤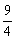 .
.
[例4]己知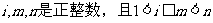
(1)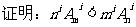
(2)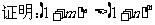
证明:(1)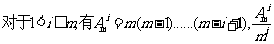
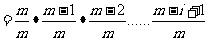
同理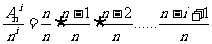
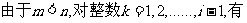
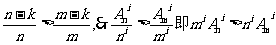
(2)由二项式定理有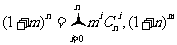
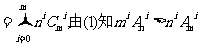
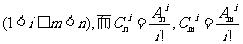
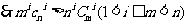
因此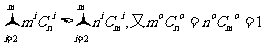
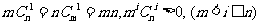
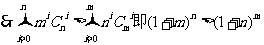 。
。
[研讨.欣赏]求证:2<(1+ )n<3(n≥2,n∈N*).
)n<3(n≥2,n∈N*).
证明:(1+ )n=C
)n=C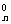 +C
+C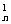 ×
× +C
+C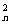 (
( )2+…+C
)2+…+C (
( )n
)n
=1+1+C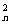 ×
×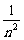 +C
+C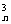 ×
×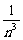 +…+C
+…+C ×
×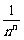
=2+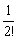 ×
×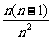 +
+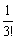 ×
×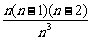 +…+
+…+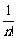 ×
×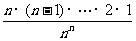
<2+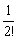 +
+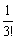 +
+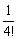 +…+
+…+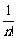 <2+
<2+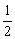 +
+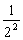 +
+ +…+
+…+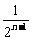
=2+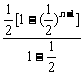 =3-(
=3-(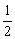 )
)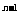 <3.
<3.
显然(1+ )n=1+1+C
)n=1+1+C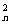 ×
×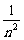 +C
+C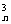 ×
×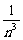 +…+C
+…+C ×
×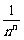 >2.所以2<(1+
>2.所以2<(1+ )n<3.
)n<3.
5. -160; 6. 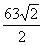 ; 7.
; 7. 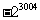 ; 8.
35; 9.
; 8.
35; 9.  ;
;
10:设 f (x) = (+x) 10 ,则(a0 + a2 + a4 + … + a10) 2-(a1 + a3 + a5 + … + a9) 2
=[(a0 + a2 + … + a10) +(a1 + a3 + … + a9) ]·[(a0 + a2 + … + a10)-(a1 + a3 + … + a9) ]
=f (1)· f (-1) = (+1)10 (-1) 10=1
4.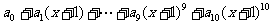
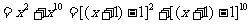
= ∴
∴ ;
;
10. 设 (+x) 10 = a0 + a1 x + a2 x 2 + … + a10 x 10,则 (a0 + a2 + a4 + … + a10) 2-(a1 + a3 + a5 + … + a9) 2 的值为 .
◆练习简答: 1-4.ABDD; 2.x的奇数次方的系数都是负值,∴只需赋值x=-1;
9.(2005天津)设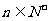 ,则
,则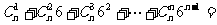 .
.
8.(2005湖南)在(1+x)+(1+x)2+……+(1+x)6的展开式中,x 2项的系数是 .(用数字作答)
7.在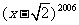 的二项展开式中,含
的二项展开式中,含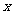 的奇次幂的项之和为
的奇次幂的项之和为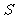 ,当
,当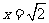 时,
时, 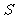 等于______;
等于______;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com