
7、函数y=Asin(ωx+φ)在一个周期上的图象如下.则函数的解析式是 ( )
 A.y=2sin(+)
A.y=2sin(+)
B.y=2sin(-)
C.y=2sin(+)
D.y=2sin(-)
6、用二分法求函数f(x)=x3+x2-2x-2的一个零点,依次计算得到下列函数值:
|
f(1)=-2 |
f(1.5)=0.625 |
|
f(1.25)=-0.984 |
f(1.375)=-0.260 |
|
f(1.438)=0.165 |
f(1.4065)=-0.052 |
那么方程x3+x2-2x-2=0的一个近似根在下列哪两数之间? ( )
A.1.25-1.375 B.1.375-1.4065
C.1.4065-1.438 D.1.438-1.5
5、函数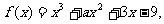 已知
已知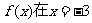 时取得极值,则
时取得极值,则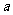 = ( )
= ( )
A.2 B.3 C.4 D.5
4、函数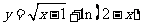 的定义域是 ( )
的定义域是 ( )
A. B.
B.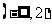 C.
C.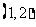 D.
D.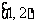
3、设曲线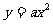 在点(1,
在点(1,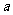 )处的切线与直线
)处的切线与直线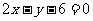 平行,则
平行,则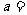 ( )
( )
A.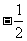 B.
B.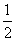 C.1 D.
C.1 D.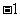
2、三个数a=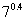 ,b=
,b=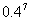 ,c=
,c=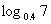 的大小顺序是 ( )
的大小顺序是 ( )
A.a>b>c B.a>c>b C.b>a>c D.c>b>a
1、设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B= ( )
A.{1,2} B.{1,5} C.{2,5} D.{1,2,5}
12. 已知1<m<n,m,n∈N*,求证:(1+m)n>(1+n)m.
证法一:由二项式定理(1+m)n=C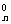 m0+C
m0+C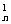 m1+…+C
m1+…+C mn,
mn,
(1+n)m=C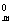 n0+C
n0+C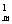 n1+…+C
n1+…+C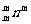 ,
,
又因为C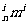 =
=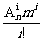 ,C
,C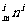 =
=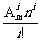 ,
,
而A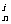 mi>A
mi>A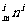 ,所以C
,所以C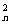 m2>C
m2>C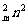 ,C
,C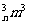 >C
>C n3,…,C
n3,…,C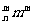 >C
>C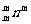 .
.
又因为C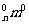 =C
=C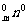 ,C
,C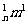 =C
=C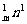 ,
,
所以(1+m)n>(1+n)m.
证法二:(1+m)n>(1+n)m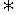 nln(1+m)>mln(1+n)
nln(1+m)>mln(1+n)
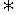
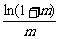 >
>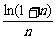 . 令f(x)=
. 令f(x)=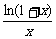 ,x∈[2,+∞],
,x∈[2,+∞],
只要证f(x)在[2,+∞]上单调递减,只要证f ′(x)<0.
f ′(x)=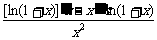 =
=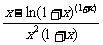 .
.
当x≥2时,x-lg(1+x)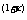 <0,
<0,
x2(1+x)>0,得f ′(x)<0,即x∈[2,+∞]时,f ′(x)<0.
以上各步都可逆推,得(1+m)n>(1+n)m.
[探索题]已知数列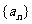 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和: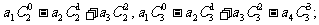
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
(3)设q≠1,Sn是等比数列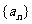 的前n项和,求:
的前n项和,求:
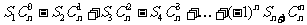 .
.
解:(1)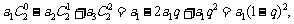
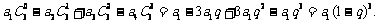
(2)归纳概括的结论为:
若数列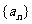 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则
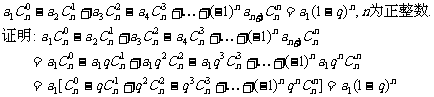
(3)因为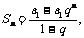

11.求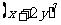 展开式中系数最大的项
展开式中系数最大的项
解:设第 项系数最大,
项系数最大,
则有 ,即
,即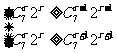

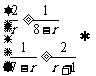

又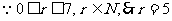
故系数最大项为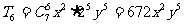
点评:二项式系数最大的项与系数最大的项不同 二项式系数最大的项也即中间项:当n为偶数时中间项
二项式系数最大的项也即中间项:当n为偶数时中间项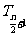 的二项式系数最大;当n为奇数时,中间两项
的二项式系数最大;当n为奇数时,中间两项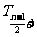 ,
,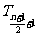 的二项式系数相等且为最大
的二项式系数相等且为最大
10.如果在(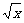 +
+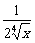 )n的展开式中,前三项系数成等差数列,求展开式中的有理项.
)n的展开式中,前三项系数成等差数列,求展开式中的有理项.
解:展开式中前三项的系数分别为1,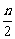 ,
,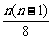 ,
,
由题意得2×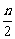 =1+
=1+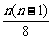 ,得n=8.
,得n=8.
设第r+1项为有理项,T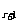 =C
=C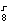 ·
·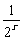 ·x
·x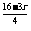 ,则r是4的倍数,所以r=0,4,8.
,则r是4的倍数,所以r=0,4,8.
有理项为T1=x4,T5=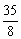 x,T9=
x,T9= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com