4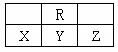．右图为周期表中短周期的一部分，若X原子最外层电子数比次外层电子数少3，则下列说法正确的是

A．X的氢化物比R的氢化物稳定

B．原子半径大小顺序是Z>Y>X>R

C．Z的单质能与Y的某些化合物发生置换反应

D．X、Z可形成化合物XZ₅，分子中各原子均满足最外层8电子结构

3．下列说法不正确的是

A．共价化合物和离子化合物中，一定都含有非金属元素

B．离子化合物中，一定既含有金属元素又含有非金属元素

C．化学变化过程，一定会破坏旧的化学键，同时形成新的化学键

D．共价化合物都是由分子构成的，而离子化合物中一般不存在单个分子

2．下列有关说法中，正确的是

A．C₄H₁₀与C₇H₁₆属于同系物　　　 　　　　B．H₂与H₃互为同位素

C．白磷和红磷互为同分异构体　　　 D．同素异形体的物理性质相同

1．从化学学科的角度分析，下列叙述不正确的是

A．绿色植物光合作用过程中的能量变化是由太阳能转变成化学能

B．研制乙醇汽油技术，可降低机动车辆尾气中有害气体的排放

C．液化石油气、天然气的主要成分都是甲烷

D．利用太阳能等清洁能源代替化石燃料，有利于节约资源、保护环境

2．已知三条直线l₁：mx－y+m＝0，l₂：x+my－m(m+1)＝0，l₃：(m+1)x－y+(m+1)＝0，它们围成△ABC.

　 (1)求证：不论m取何值时，△ABC中总有一个顶点为定点；

　 (2)当m取何值时，△ABC的面积取最大值、最小值？并求出最大值、最小值．

　 解答：(1)证明：设直线l₁与直线l₃的交点为A，

　 由

　 得x＝－1，y＝0，∴A点坐标为(－1,0)，∴不论m取何值△ABC中总有一个顶点A(－1,0)为定点．

　 (2)由

　 得x＝0，y＝m+1，即l₂与l₃交点为(0，m+1)，

　 由

　 得x＝，y＝，即l₁与l₂交点为(，)，

　 ∴S_△ABC＝··

　 ＝＝(2－)

　 ∵m²+1≥1，∴1≤2－<2，∴≤(2－)<1即≤S_△ABC<1，

　 ∴当m＝0时S_△ABC取到最小值，S_△ABC取不到最大值．

1．k为何值时，直线l₁：y＝kx+3k－2与直线l₂：x+4y－4＝0的交点在第一象限．

　 解答：由，得

　 ∵两直线的交点在第一象限，

　 ∴，∴<k<1.

　 即当＜k＜1时，两直线的交点在第一象限．

10．已知直线l过P(3，－2)点，求：

　 (1)原点到直线l距离最大的l的方程；

　 (2)原点到直线l距离为3的l的方程．

　 解答：(1)∵k_OP＝－，∴直线l的斜率为k＝－＝.

　 则直线l的方程为y+2＝(x－3)，即3x－2y－13＝0.

　 (2)设所求直线的方程为y+2＝k(x－3)，即kx－y－3k－2＝0.

　 由＝3，解得k＝，则l的方程为5x－12y－39＝0，

　 又斜率不存在时的直线方程x＝3符合题意，

　 因此直线l的方程为x＝3或5x－12y－39＝0.

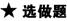
9．在直角梯形OABC中，OA∥BC，OA⊥OC，在OA、BC边上分别有两点P、Q，若PQ平分梯形的面积，求证：直线PQ必过一定点．

　 证明：如图所示，以OA所在直线为x轴，O为原点，建立坐标系

　 设A、B、P、Q的坐标分别为(a,0)、(b，c)、(t_1,0)、(t₂，c)，

　 ∴直线PQ的方程为：y＝(x－t₁)．

　 由PQ平分梯形ABCO的面积，∴2S_梯形PQCO＝S_梯形ABCO.

　 即2·＝，∴t₁+t₂＝，即t₂＝－t₁.

　 直线PQ的方程为y＝(x－t₁)，

　 整理得：2cx－(a+b－4t₁)y－2ct₁＝0

　 即(4y－2c)t₁+2cx－(a+b)y＝0，∴y＝，x＝.

　 因此直线PQ必过定点(，)．

8．求过点P(1,2)且与A(2,3)和B(4，－5)等距离的直线方程．

　 解答：解法一：所求直线有两条，一条是过P(1,2)点且过AB的中点，另一条是过P(1,2)与A、B两点所确定的直线平行．

　 AB的中点M的坐标为(3，－1)，∴过P、M两点的直线方程为y－2＝(x－1)，

　 整理得3x+2y－7＝0；

　 过P点与AB平行的直线为y－2＝(x－1)，

　 整理得4x+y－6＝0；

　 因此所求的直线方程为3x+2y－7＝0，或4x+y－6＝0.

　 解法二：设所求的直线方程为y－2＝k(x－1)，

　 即kx－y+2－k＝0，

　 根据题意：＝，

　 即|k－1|＝|3k+7|，解得：k＝－4或k＝－.

　 因此所求的直线方程分别为4x+y－6＝0或3x+2y－7＝0.

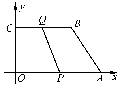
7．在△ABC中，BC边上的高所在直线方程为x－2y+1＝0，∠A的平分线所在的直线为y＝0，点B(1,2)，则点A和点C的坐标分别是________．

　 解析：由得顶点A(－1,0)，k_AB＝1，

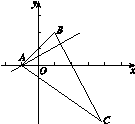
　 ∴k_AC＝－1，∴AC方程为y＝－x－1.①

　 又BC方程y＝－2x+4，②

　 解①和②得C(5，－6)．

　 答案：(－1,0)，(5，－6)