
6、定义在R上的函数y=f(x)有反函数y=f -1(x),则y=f(x+a)+b与y=f -1(x+a)+b关于 对称。
简答精讲:1-4、CBAD;5、-2;4;6、y=x+a+b
5、(2005湖南)设函数f(x)的图象关于点(1,2)对称,且存在反函数f-1(x),f (4)=0,则f-1(4)= .
4.定义在R上的函数f(x)的最小正周期是T,且y=f(x),x∈(0,T)的反函数是y=f -1(x),x∈M,则函数y=f(x),x∈(2T,3T)的反函数为( )
A.y=f -1(x) (x∈M), B.y=f -1(x-2T) (x∈M)
C. .y=f -1(x+2T) (x∈M) D. .y=f -1(x)+2T (x∈M)
3、函数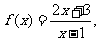
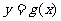 的图象与
的图象与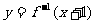 的图象关于直线
的图象关于直线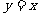 对称,则g(11)等于 ( )
对称,则g(11)等于 ( )
A.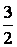 B.
B.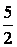 C.
C.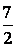 D.
D.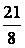
2、 (2005全国Ⅱ)函数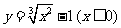 的反函数是( )
的反函数是( )
A.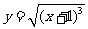 (
(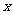 ≥-1) B.
≥-1) B.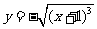 (
(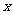 ≥-1)
≥-1)
C.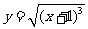 (
(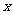 ≥0) d.
≥0) d.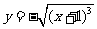 (
(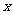 ≥0)
≥0)
1、(2005全国Ⅰ)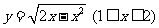 反函数是( )A.
反函数是( )A.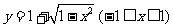 B.
B.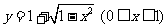
C.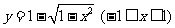 D.
D.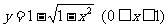
4.单调函数必有反函数;互为反函数的单调性一致;奇函数如果有反函数必为奇函数。
3.互为反函数图象间的关系:
互为反函数的两个函数y=f(x)与y=f-1(x)在同一直角坐标系中的图象关于直线y=x对称.
注意:x=f -1(y)表示的图象与y=f(x)的图象相同。
2.求反函数的步骤:
(1)由y=f(x)解得x=f-1(y).
(2)确定原函数的值域,即反函数的定义域;
(3)把x=f-1(y)中的x、y互换,写出反函数,(及定义域)
1.反函数概念:若函数y=f(x)(x∈A)的值域为C,由y=f(x)解得x=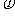 (y).如果对于任何y∈C,通过x=
(y).如果对于任何y∈C,通过x=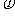 (y),在A中都有唯一的x和它对应,那么x=
(y),在A中都有唯一的x和它对应,那么x=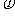 (y)就叫做函数y=f(x)(x∈A)的反函数,记作x=f-1(y)y∈C是自变量,x是自变量y的函数.
(y)就叫做函数y=f(x)(x∈A)的反函数,记作x=f-1(y)y∈C是自变量,x是自变量y的函数.
习惯上,一般用x表示自变量,y表示函数,因此我们常对调x=f-1(y)中的x、y,把它改写成y=f-1(x)(x∈C)
由反函数定义知:①b=f(a)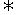 a=f-1(b),②f[f-1(x)]=x(x∈C);
f-1[f(x)]=x(x∈A).
a=f-1(b),②f[f-1(x)]=x(x∈C);
f-1[f(x)]=x(x∈A).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com