
3、(2005天津)设函数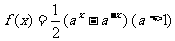 的反函数是
的反函数是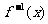 ,则使
,则使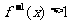 成立的x的取值范围为 ( )
成立的x的取值范围为 ( )
A.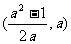 B.
B.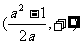 C.
C.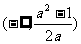 D.
D.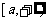
[填空题]
2、(2006辽宁)与方程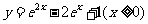 的曲线关于直线
的曲线关于直线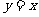 对称的曲线的方程为
( )
对称的曲线的方程为
( )
(A)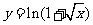 (B)
(B)
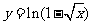
(C) 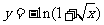 (D)
(D)
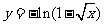
1.(2005江苏卷)函数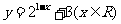 的反函数的解析表达式为( )
的反函数的解析表达式为( )
(A)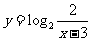 (B)
(B)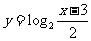
(C)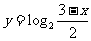 (D)
(D)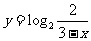
3、互为反函数性质及图象间的关系--
同步练习 2.8反函数
[选择题]
2、求反函数的步骤--
1、反函数定义--
[例1]求下列函数的反函数:
(1) ;(2)
;(2)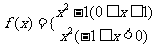 ;
;
(3)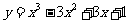 ;
;
解:(1)由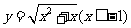 得
得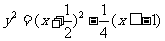 ,
,
∴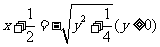 ,
,
∴所求函数的反函数为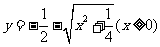 ;
;
(2)当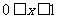 时,
时,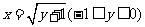 ,当
,当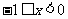 时,
时,
得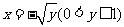 ,
,
∴所求函数的反函数为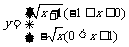
(3)由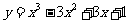 得
得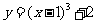 ,
,
∴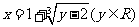 ,
,
∴所求反函数为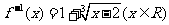 .
.
提炼方法:1.求反函数的步骤:
2.分段函数的反函数要分段求. 并注意原函数在每段上的值域.
[例2]已知函数f(x)=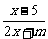 的图象关于直线y=x对称,求实数m.
的图象关于直线y=x对称,求实数m.
解:∵f(x)的图象关于直线y=x对称,又点(5,0)在f(x)的图象上,∴点(0,5)也在f(x)的图象上,即-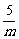 =5,得m=-1.
=5,得m=-1.
法二:由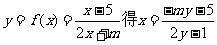 ,有反函数
,有反函数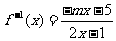 。由于f(x)的图象关于y=x对称,与f -1(x)相同,比较系数得m=-1.
。由于f(x)的图象关于y=x对称,与f -1(x)相同,比较系数得m=-1.
提炼方法:法1.找一特殊点(5,0)的对称点在图象上;
法2.f(x) 与f -1(x)相同,比较系数.
[例3]已知函数f(x)=2(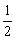 -
-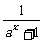 )(a>0,且a≠1).
)(a>0,且a≠1).
(1)求反函数y=f-1(x);
(2)判定f-1(x)的奇偶性;
(3)解不等式f-1(x)>1.
解:(1)化简,得f(x)=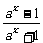 .
.
设y=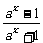 ,则ax=
,则ax=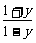 .∴x=loga
.∴x=loga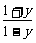 .
.
∴所求反函数为
y=f-1(x)=loga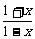 (-1<x<1).
(-1<x<1).
(2)∵f-1(-x)=loga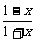 =loga(
=loga(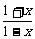 )-1=-loga
)-1=-loga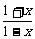 =-f-1(x),
=-f-1(x),
∴f-1(x)是奇函数.
(3)loga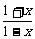 >1.
>1.
当a>1时,
原不等式
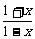 >a
>a
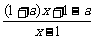 <0.
<0.
∴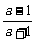 <x<1.
<x<1.
当0<a<1时,原不等式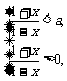
解得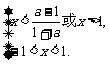
∴-1<x<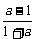 .
.
综上,当a>1时,所求不等式的解集为(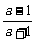 ,1);
,1);
当0<a<1时,所求不等式的解集为(-1,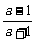 ).
).
[研究.欣赏]
已知函数f(x)是函数y=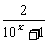 -1(x∈R)的反函数,函数g(x)的图象与函数y=
-1(x∈R)的反函数,函数g(x)的图象与函数y=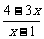 的图象关于直线y=x-1成轴对称图形,记F(x)=f(x)+g(x).
的图象关于直线y=x-1成轴对称图形,记F(x)=f(x)+g(x).
(1)求F(x)的解析式及定义域.
(2)试问在函数F(x)的图象上是否存在这样两个不同点A、B,使直线AB恰好与y轴垂直?若存在,求出A、B两点坐标;若不存在,说明理由.
解:(1)由y=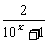 -1(x∈R),得10x=
-1(x∈R),得10x=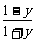 ,x=lg
,x=lg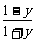 .∴f(x)=lg
.∴f(x)=lg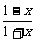 (-1<x<1).
(-1<x<1).
设P(x,y)是g(x)图象上的任意一点,则P关于直线y=x-1的对称点P′的坐标为(1+y,x-1).由题设知点P′(1+y,x-1)在函数y=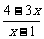 的图象上,∴x-1=
的图象上,∴x-1=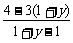 .
.
∴y=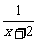 ,即g(x)=
,即g(x)=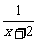 (x≠-2).
(x≠-2).
∴F(x)=f(x)+g(x)=lg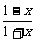 +
+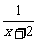 ,其定义域为{x|-1<x<1}.
,其定义域为{x|-1<x<1}.
(2)∵f(x)=lg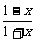 =lg(-1+
=lg(-1+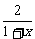 )(-1<x<1)是减函数,g(x)=
)(-1<x<1)是减函数,g(x)=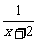 (-1<x<1)也是减函数,∴F(x)在(-1,1)上是减函数.
(-1<x<1)也是减函数,∴F(x)在(-1,1)上是减函数.
故不存在这样两个不同点A、B,使直线AB恰好与y轴垂直.
点评:本题是一道综合题,解决第(2)小题常用的方法是反证法,但本题巧用单调性法使问题变得简单明了.
6、y=f(x+a)+b与y=f -1(x+a)+b是y=f(x)与y=f -1(x)按向量(-a,b)平移而得,所以对称轴也跟着平移,变为y=x+a+b
5、由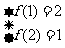 得
得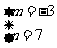 ;
;
3、设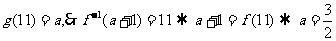
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com