
2.指数函数的图象和性质:
在同一坐标系中分别作出函数y=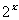 ,y=
,y=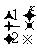 ,y=
,y=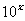 ,y=
,y=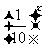 的图象.
的图象.
列表如下:
|
x |
… |
-3 |
-2 |
-1 |
-0.5 |
0 |
0.5 |
1 |
2 |
3 |
… |
y=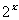 |
… |
0.13 |
0.25 |
0.5 |
0.71 |
1 |
1.4 |
2 |
4 |
8 |
… |
y= |
… |
8 |
4 |
2 |
1.4 |
1 |
0.71 |
0.5 |
0.25 |
0.13 |
… |
|
x |
… |
-1.5 |
-1 |
-0.5 |
-0.25 |
0 |
0.25 |
0.5 |
1 |
1.5 |
… |
y=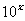 |
… |
0.03 |
0.1 |
0.32 |
0.56 |
1 |
1.78 |
3.16 |
10 |
31.62 |
… |
y=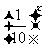 |
… |
31.62 |
10 |
3.16 |
1.78 |
1 |
0.56 |
0.32 |
0.1 |
0.03 |
… |
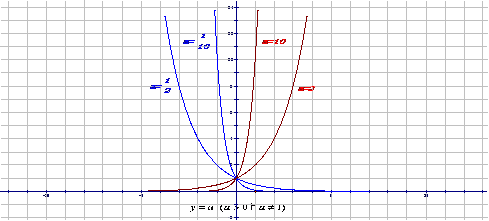
我们观察y=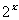 ,y=
,y=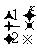 ,y=
,y=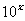 ,y=
,y=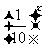 的图象特征,就可以得到
的图象特征,就可以得到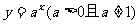 的图象和性质
的图象和性质
|
|
a>1 |
0<a<1 |
|
图 象 |
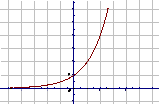 |
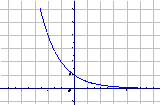 |
|
性 质 |
(1)定义域:R |
|
|
(2)值域:(0,+∞) |
||
|
(3)过点(0,1),即x=0时,y=1 |
||
|
(4)在 R上是增函数 |
(4)在R上是减函数 |
1.指数函数的定义:
函数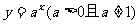 叫做指数函数,其中x是自变量,函数定义域是R
叫做指数函数,其中x是自变量,函数定义域是R
探究1:为什么要规定a>0,且a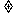 1呢?
1呢?
①若a=0,则当x>0时,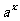 =0;当x
=0;当x 0时,
0时,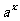 无意义.
无意义.
②若a<0,则对于x的某些数值,可使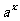 无意义. 如
无意义. 如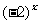 ,这时对于x=
,这时对于x=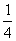 ,x=
,x=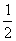 ,…等等,在实数范围内函数值不存在.
,…等等,在实数范围内函数值不存在.
③若a=1,则对于任何x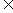 R,
R,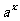 =1,是一个常量,没有研究的必要性.
=1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且a¹1在规定以后,对于任何x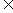 R,
R,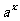 都有意义,且
都有意义,且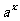 >0. 因此指数函数的定义域是R,值域是(0,+∞).
>0. 因此指数函数的定义域是R,值域是(0,+∞).
探究2:函数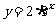 是指数函数吗?
是指数函数吗?
指数函数的解析式y=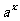 中,
中,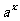 的系数是1.
的系数是1.
有些函数貌似指数函数,实际上却不是,如y=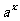 +k
(a>0且a
+k
(a>0且a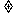 1,k
1,k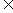 Z);有些函数看起来不像指数函数,实际上却是,如y=
Z);有些函数看起来不像指数函数,实际上却是,如y=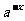 (a>0,且a
(a>0,且a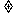 1),因为它可以化为y=
1),因为它可以化为y=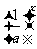 ,其中
,其中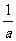 >0,且
>0,且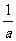
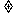 1
1
引例1(P57):某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数关系是什么?
分裂次数:1,2,3,4,…,x
细胞个数:2,4,8,16,…,y
由上面的对应关系可知,函数关系是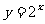 .
.
引例2:某种商品的价格从今年起每年降低15%,设原来的价格为1,x年后的价格为y,则y与x的函数关系式为 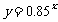
在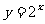 ,
,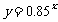 中指数x是自变量,底数是一个大于0且不等于1的常量.
中指数x是自变量,底数是一个大于0且不等于1的常量.
我们把这种自变量在指数位置上而底数是一个大于0且不等于1的常量的函数叫做指数函数.
第二节 书面表达(满分30分)
假如你是高三学生李华,在毕业前的一堂英语课上,英语老师要求你们每人做一个简短的演讲,请你根据以下提示用英语写一篇演讲稿。
1.最难忘的一次经历;
2.所取得的优异成绩;
3.你对未来的展望。
注意:
1.词数100左右;
2.可适当增加细节以使行文连贯;
3.开头和结尾已给出;不计入总词数。
Hello, everyone!
I’m glad to make a speech here.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com