
3.关于物体的运动,不可能发生的是( )
A.加速度大小逐渐减小,速度也逐渐减小
B.加速度方向不变,而速度方向改变
C.加速度和速度都在变化,加速度最大时,速度最小
D.加速度为零时,速度的变化率最大
2.某质点做变速运动,初始的速度为 3 m/s,经3 s速率仍为 3 m/s测( )
A.如果该质点做直线运动,该质点的加速度不可能为零
B.如果该质点做匀变速直线运动,该质点的加速度一定为 2 m/s2
C.如果该质点做曲线运动,该质点的加速度可能为 2 m/s2
D.如果该质点做直线运动,该质点的加速度可能为 12 m/s2
1.对于质点的运动,下列说法中正确的是( )
A.质点运动的加速度为零,则速度为零,速度变化也为零
B.质点速度变化率越大,则加速度越大
C.质点某时刻的加速度不为零,则该时刻的速度也不为零
D.质点运动的加速度越大,它的速度变化越大
[例5]关于位移和路程,下列说法中正确的是( )
A.物体沿直线向某一方向运动,通过的路程就是位移
B.物体沿直线向某一方向运动,通过的路程等于位移的大小
C.物体通过一段路程,其位移可能为零
D.物体通过的路程可能不等,但位移可能相同
解析:位移是矢量,路程是标量,不能说这个标量就是这个矢量,所以A错,B正确.路程是物体运动轨迹的实际长度,而位移是从物体运动的起始位置指向终止位置的有向线段,如果物体做的是单向直线运动,路程就和位移的大小相等.如果物体在两位置间沿不同的轨迹运动,它们的位移相同,路程可能不同.如果物体从某位置开始运动,经一段时间后回到起始位置,位移为零,但路程不为零,所以,CD正确.
[例6]关于速度和加速度的关系,下列说法中正确的是()
A.速度变化越大,加速度就越大
B.速度变化越快,加速度越大
C.加速度大小不变,速度方向也保持不变
C.加速度大小不断变小,速度大小也不断变小
解析:根据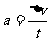 可知,Δv越大,加速度不一定越大,速度变化越快,则表示
可知,Δv越大,加速度不一定越大,速度变化越快,则表示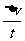 越大,故加速度也越大,B正确.加速度和速度方向没有直接联系,加速度大小不变,速度方向可能不变,也可能改变.加速度大小变小,速度可以是不断增大.故此题应选B.
越大,故加速度也越大,B正确.加速度和速度方向没有直接联系,加速度大小不变,速度方向可能不变,也可能改变.加速度大小变小,速度可以是不断增大.故此题应选B.
[例7 ]在与x轴平行的匀强电场中,场强为E=1.0×106V/m,一带电量q=1.0×10-8C、质量m=2.5×10-3kg的物体在粗糙水平面上沿着x轴作匀速直线运动,其位移与时间的关系是x=5-2t,式中x以m为单位,t以s为单位。从开始运动到5s末物体所经过的路程为 m,位移为 m。
解析:须注意本题第一问要求的是路程;第二问要求的是位移。
将x=5-2t和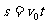 对照,可知该物体的初位置x0=5m,初速度v0=
对照,可知该物体的初位置x0=5m,初速度v0= m/s,运动方向与位移正方向相反,即沿x轴负方向,因此从开始运动到5s末物体所经过的路程为10m,而位移为
m/s,运动方向与位移正方向相反,即沿x轴负方向,因此从开始运动到5s末物体所经过的路程为10m,而位移为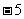 m。
m。
[例8]某游艇匀速滑直线河流逆水航行,在某处丢失了一个救生圈,丢失后经t秒才发现,于是游艇立即返航去追赶,结果在丢失点下游距丢失点s米处追上,求水速.(水流速恒定,游艇往返的划行速率不变)。
解析:以水为参照物(或救生圈为参照物),则游艇相对救生圈往返的位移大小相等,且游艇相对救生圈的速率也不变,故返航追上救生圈的时间也为t秒,从丢失到追上的时间为2t秒,在2t秒时间内,救生圈随水运动了s米,故水速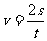
思考:若游艇上的人发现丢失时,救生圈距游艇s米,此时立即返航追赶,用了t秒钟追上,求船速.
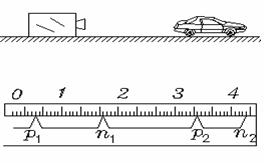 [例9]如图所示为高速公路上用超声测速仪测车速的示意图,测速仪发出并接收超声波脉冲信号,根据发出和接收到信号间的时间差,测出被测物体速度,图中P1、P2是测速仪发出的超声波信号,n1、n2分别是P1、P2被汽车反射回来的信号,设测速仪匀速扫描,P1,P2之间的时间间隔Δt=1.0s,超声波在空气中传播的速度是340m/s,若汽车是匀速行驶的,则根据图B可知汽车在接收P1、P2两个信号之间的时间内前进的距离是___m,汽车的速度是_____m/s.
[例9]如图所示为高速公路上用超声测速仪测车速的示意图,测速仪发出并接收超声波脉冲信号,根据发出和接收到信号间的时间差,测出被测物体速度,图中P1、P2是测速仪发出的超声波信号,n1、n2分别是P1、P2被汽车反射回来的信号,设测速仪匀速扫描,P1,P2之间的时间间隔Δt=1.0s,超声波在空气中传播的速度是340m/s,若汽车是匀速行驶的,则根据图B可知汽车在接收P1、P2两个信号之间的时间内前进的距离是___m,汽车的速度是_____m/s.
解析:本题首先要看懂B图中标尺所记录的时间每一小格相当于多少:由于P1 P2 之间时间间隔为1.0s,标尺记录有30小格,故每小格为1/30s,其次应看出汽车两次接收(并反射)超声波的时间间隔:P1发出后经12/30s接收到汽车反射的超声波,故在P1发出后经6/30s被车接收,发出P1后,经1s发射P2,可知汽车接到P1后,经t1=1-6/30=24/30s发出P2,而从发出P2到汽车接收到P2并反射所历时间为t2=4.5/30s,故汽车两次接收到超声波的时间间隔为t=t1+t2=28.5/30s,求出汽车两次接收超声波的位置之间间隔:s=(6/30-4.5/30)v声=(1.5/30)×340=17m,故可算出v汽=s/t=17÷(28.5/30)=17.9m/s.
[例10] 天文观测表明,几乎所有远处的恒星(或星系)都在以各自的速度远离我们而运动,离我们越远的星体,背离我们运动的速度(称为退行速度)越大;也就是说,宇宙在膨胀,不同星体的退行速度v和它们离我们的距离r成正比,即v=Hr,式中H为一恒量,称为哈勃常数,已由天文观测测定。为解释上述现象,有人提出一种理论,认为宇宙是从一个爆炸的大火球开始形成的,大爆炸后各星体即以各自不同的速度向外匀速运动,并设想我们就位于其中心。由上述理论和天文观测结果,可估算宇宙年龄T,其计算式为T= 。根据近期观测,哈勃常数H=3×10-2m/s﹒光年,由此估算宇宙的年龄约为 年。
解析:本题涉及关于宇宙形成的大爆炸理论,是天体物理学研究的前沿内容,背景材料非常新颖,题中还给出了不少信息。题目描述的现象是:所有星体都在离我们而去,而且越远的速度越大。提供的一种理论是:宇宙是一个大火球爆炸形成的,爆炸后产生的星体向各个方向匀速运动。如何用该理论解释呈现的现象?可以想一想:各星体原来同在一处,现在为什么有的星体远,有的星体近?显然是由于速度大的走得远,速度小的走的近。所以距离远是由于速度大,v=Hr只是表示v与r的数量关系,并非表示速度大是由于距离远。
对任一星体,设速度为v,现在距我们为r,则该星体运动r这一过程的时间T即为所要求的宇宙年龄,T=r/v
将题给条件v=Hr代入上式得宇宙年龄 T=1/H
将哈勃常数H=3×10-2m/s·光年代入上式,得T=1010年。
点评:有不少考生遇到这类完全陌生的、很前沿的试题,对自己缺乏信心,认为这样的问题自己从来没见过,老师也从来没有讲过,不可能做出来,因而采取放弃的态度。其实只要静下心来,进入题目的情景中去,所用的物理知识却是非常简单的。这类题搞清其中的因果关系是解题的关键。
2.图像:匀速直线运动的s - t图像为一直线:图线的斜率在数值上等于物体的速度。
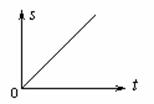
1.定义: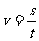 ,即在任意相等的时间内物体的位移相等.它是速度为恒矢量的运动,加速度为零的直线运动。
,即在任意相等的时间内物体的位移相等.它是速度为恒矢量的运动,加速度为零的直线运动。
6、运动的相对性:只有在选定参考系之后才能确定物体是否在运动或作怎样的运动。一般以地面上不动的物体为参照物。
[例3]甲向南走100米的同时,乙从同一地点出发向东也行走100米,若以乙为参考系,求甲的位移大小和方向?
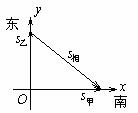
解析:如图所示,以乙的矢量末端为起点,向甲的矢量末端作一条有向线段,即为甲相对乙的位移,由图可知,甲相对乙的位移大小为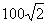 m,方向,南偏西45°。
m,方向,南偏西45°。
点评:通过该例可以看出,要准确描述物体的运动,就必须选择参考系,参考系选择不同,物体的运动情况就不同。参考系的选取要以解题方便为原则。在具体题目中,要依据具体情况灵活选取。下面再举一例。
[例4]某人划船逆流而上,当船经过一桥时,船上一小木块掉在河水里,但一直航行至上游某处时此人才发现,便立即返航追赶,当他返航经过1小时追上小木块时,发现小木块距离桥有5400米远,若此人向上和向下航行时船在静水中前进速率相等。试求河水的流速为多大?
解析:选水为参考系,小木块是静止的;相对水,船以恒定不变的速度运动,到船“追上”小木块,船往返运动的时间相等,各为1 小时;小桥相对水向上游运动,到船“追上”小木块,小桥向上游运动了位移5400m,时间为2小时。易得水的速度为0.75m/s。
5、加速度:描述物体速度变化快慢的物理量,a=△v/△t (又叫速度的变化率),是矢量。a的方向只与△v的方向相同(即与合外力方向相同)。
点评1:
(1)加速度与速度没有直接关系:加速度很大,速度可以很小、可以很大、也可以为零(某瞬时);加速度很小,速度可以很小、可以很大、也可以为零(某瞬时)。
(2)加速度与速度的变化量没有直接关系:加速度很大,速度变化量可以很小、也可以很大;加速度很小,速度变化量可以很大、也可以很小。加速度是“变化率”--表示变化的快慢,不表示变化的大小。
点评2:物体是否作加速运动,决定于加速度和速度的方向关系,而与加速度的大小无关。加速度的增大或减小只表示速度变化快慢程度增大或减小,不表示速度增大或减小。
(1)当加速度方向与速度方向相同时,物体作加速运动,速度增大;若加速度增大,速度增大得越来越快;若加速度减小,速度增大得越来越慢(仍然增大)。
(2)当加速度方向与速度方向相反时,物体作减速运动,速度减小;若加速度增大, 速度减小得越来越快;若加速度减小,速度减小得越来越慢(仍然减小)。
[例2]一物体做匀变速直线运动,某时刻速度大小为4m/s,经过1s后的速度的大小为10m/s,那么在这1s内,物体的加速度的大小可能为
解析:本题考查速度、加速度的矢量性。经过1s后的速度的大小为10m/s,包括两种可能的情况,一是速度方向和初速度方向仍相同,二是速度方向和初速度方向已经相反。取初速度方向为正方向,则1s后的速度为vt=10m/s 或vt =-10m/s
由加速度的定义可得
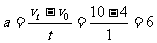 m/s或
m/s或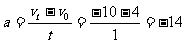 m/s。
m/s。
答案:6m/s或14m/s
点评:对于一条直线上的矢量运算,要注意选取正方向,将矢量运算转化为代数运算。
4、速度:描述物体运动快慢和运动方向的物理量,是位移对时间的变化率,是矢量。
平均速度:在变速直线运动中,运动物体的位移和所用时间的比值,v = s/t(方向为位移的方向)
瞬时速度:对应于某一时刻(或某一位置)的速度,方向为物体的运动方向。
速率:瞬时速度的大小即为速率;
平均速率:质点运动的路程与时间的比值,它的大小与相应的平均速度之值可能不相同。
注意:平均速度的大小与平均速率的区别.
[例1]物体M从A运动到B,前半程平均速度为v1,后半程平均速度为v2,那么全程的平均速度是:( )
A.(v1+v2)/2 B.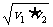 C.
C.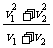 D.
D.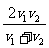
解析:本题考查平均速度的概念。全程的平均速度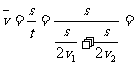
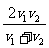 ,故正确答案为D
,故正确答案为D
3、位置:表示空间坐标的点。
位移:由起点指向终点的有向线段,位移是末位置与始位置之差,是矢量。
路程:物体运动轨迹之长,是标量。
注意:位移与路程的区别.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com