2．函数的积的导教

　 法则：两个函数的积的导数，等于第一个函数的导数乘以第二个函数，加上第一个函数乘以第二个函数的导数，即　 (uv)’＝u’v+v’u.

1．函数的和或差的导数

法则：两个函数的和或差的导数，等于两个函数的导数的和或差，即(u±v)’＝u’±v’.

3．导数的几何意义：函数y=f(x)在点x0处的导数的几何意义，就是曲线y=f(x)在P(x0，f(x0))处的切线的斜率，即曲线y=f(x)在点P(x0，f(x0))处的切线斜率为k＝f ’(x0)．函数 y＝f(x)在点 P(x0，f(x0))处的切线方程为 y－y0=f ’(x0)·(x－x0)．函数y=f(x)在点P(x0，f(x0))处的法线方程为y－y0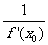＝－(x－x0)或x＝x0.

(2)常见函数的导数：

(c)’=0, (c为常数)；(xm)’=mx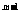；(sinx)’=cosx；

(cosx)’=－sinx；(ex)’=ex；(ax)’=ax·lna；(lnx)’=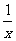；(ligax)’=.

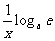(3)导数的运算：

2．导函数：如果函数y=f(x)在区间(a，b)内每一点都可导，就说y=f(x)在区间(a，b)内可导．即对于开区间(a，b)内每一个确定的x0值，都相对应着一个确定的导数f ’(x0)，这样在开区间(a，b)内构成一个新函数，把这一新函数叫做f(x)在(a，b)内的导函数．简称导数．记作f ’(x)或y’.

即f ’(x)=y’==。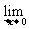

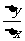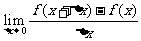(1)导数的概念：

1．导数的定义：对函数y=f(x)，在点x=x0处给自变量x以增量x，函数y相应有增量y=f(x0+x)－f(x0)，若极限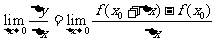存在，则此极限称为f(x)在点x=x0处的导数，记为f ’(x0)，或y’|；

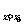3、 将本课所得认识与感受写下来。

2、 预习16课。

1、 完成“伴你学”中本课内容。

2、 说一说：学完本文后，你对体育、对心中的体育名星产生了哪些新的认识或感受？

学生各抒己见

1、 讨论“练习三”