
1.06 g m1(Na2CO3·10H2O) m1(H2O)
m1(Na2CO3·10H2O)=2.86 g m1(H2O)=1.80 g
再求溶解在1.80 g水中Na2CO3的质量m2(Na2CO3),及这些Na2CO3析出所形成晶体的质量m2(Na2CO3·10H2O)和溶液由此而减少水的质量m2(H2O)
m2(Na2CO3)=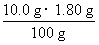 =0.180
g
=0.180
g
Na2CO3 - Na2CO3·10H2O - 10H2O
106 g 286 g 180 g
(一)学习方法点拨
1.导数的概念:
设f(x)在点x=x0 附近有定义,若极限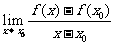 存在,则称其为f(x)在点x=x0处的导数f ’(x0).可以证明这一结论与教科书上的导数定义是等价的.
存在,则称其为f(x)在点x=x0处的导数f ’(x0).可以证明这一结论与教科书上的导数定义是等价的.
另外,若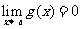 ,且存在a的邻域(α,β),当x∈(α, x0)∪(x0, β)时,有g(x)≠0,则
,且存在a的邻域(α,β),当x∈(α, x0)∪(x0, β)时,有g(x)≠0,则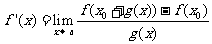 ,又若
,又若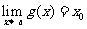 ,且存在a的邻域(α,β),当x∈(α, x0)∪(x0, β)时,有g(x)≠x0,则
,且存在a的邻域(α,β),当x∈(α, x0)∪(x0, β)时,有g(x)≠x0,则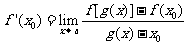 .
.
设f(x)=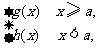 那么g(a)=h(a)=A,且
那么g(a)=h(a)=A,且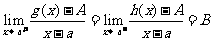
为f(x)在点x=a处可导的充要条件,此时f ’(a)=B.
由此可知,若分段函数f(x)的表达式中的g(x)、h(x)可分别看做含有a的区间(α,β)上的函数,且g(a)=h(a),g’(a)=h’(a),则f(x)在点x=a处可导;且有f ’(a)==g’(a)=h’(a).
2.曲线的切线:
设曲线S:y=f(x),若f ’(x0)存在,则S在点P(x0,f(x0)处的切线方程为
l:y-f(x0)=f’(x0)(x-x0).
可见l的方程被x0所唯一确定;若f(x)在区间(α,β)内可导,则当点x0在(α,β)内变动时,点P(x0,f(x0))在S上变动,而l“贴着”曲线S转动.所以要求具有某种性质的切线,可转化为这种性质对点x0的要求,解出x0,即可求出对应的切线方程.
应当了解可能一曲线在某点处不可导;但在这一点的切线还是存在的,例如曲线y=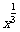 在点x=0处不可导,但在原点处有切线x=0.
在点x=0处不可导,但在原点处有切线x=0.
3.导数运算
要熟练掌握基本导数公式以及函数的和、差、积、商的求导法则.
对复合函数求导法则,应首先搞清楚函数的复合过程,方法是研究运算顺序,例如给定函数y=ln(sinex),所谓运算顺序是指对自变量x,应先计算u=ex,再计算v=sinu,最后算出y=lnv,然后倒过来即得复合过程y=lnv,v=sinu,u=ex,从而有y’=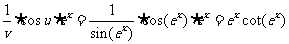 .
.
对复合函数求导法则的掌握,要熟练到可以不写出复合过程而直接写出求导结果.
4.函数的单调性
应当理解函数的单调性与可导性并无本质的联系,甚至具有单调性的函数并不一定连续.我们只是利用可导来研究单调性,这样就将研究的范围局限于可导函数.
f(x)在区间I上可导,那么f ’(x)> 0是f(x)为增函数的充分条件,例如f(x)=x3是定义于R的增函数,但f ’(0)=0,这说明f ’(x)>0非必要条件.
我们也可利用导数来证明一些不等式.如f(x)、g(x)均在[a、b]上连续,(a,b)上可导,那么令h(x)=f(x)-g(x),则h(x)也在[a,b]上连续,且在(a,b)上可导,若对任何x∈(a,b)有 h’(x)>0且 h(a)≥0,则当x∈(a,b)时 h(x)>h(a)=0,从而f(x)>g(x)对所有x∈(a,b)成立.
5.可导函数的极值
从函数的极值定义看,极值的存在与可微性无必然联系.如f(x)=|x-1|,易见当x=1时f(x)取得极小值,但f ’(1)不存在.所以用研究导数的方法探求函数的极值,实际上是将研究的范围局限于可导函数.
对可导函数f(x),在x=x0取极值的必要条件是f(x0)=0.又设f(x)在点x=x0处取得极小值,是否一定存在x0的邻域(α,β),使当x∈(α,x0)时f ’(x)<0,且当x∈(x0,β)时f ’(x)>0,答案是否定的,即f ’(x)在x0的“左侧附近”为负,且在x0“右侧附近”为正仅是f(x0)为极小值的充分条件,为说明这一情况,我们考察函数f(x)=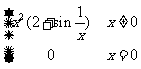 ,由于
,由于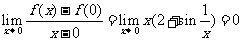 ,故有
,故有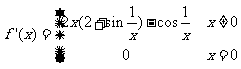 ,
,
即f(x)在R上可导.又当x≠0时f(x)>0,而f(0)=0,故当x=0时f(x)取得极小值0,但对任何α<0,总可取到充分小的 k∈Z,使
x1=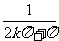 ∈(α,0),且f ’(x1)=
∈(α,0),且f ’(x1)=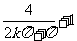 >0,又对任何β>0,总可取到充分大的k∈Z,使x2=
>0,又对任何β>0,总可取到充分大的k∈Z,使x2=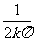 ∈(0,β),且f ’(x2)=
∈(0,β),且f ’(x2)=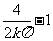 <0.
<0.
6.函数的最大值与最小值
函数的极值是“局部性质”,例如极小值点是指存在一个邻域,在其中此点的函数值最小,而函数的最大值、最小值是“全局性质”,即在函数的整体定义域内的某点处函数值最大(小),这两个概念是有区别的.但它们也有联系,即当最大(小)值点在区间内部时,它当然也是极值点,所以求定义于区间[a,b]上的函数f(x)的最大(小)值时,只需此较诸极值与区间端点处的函数值f(x)、f(b)即可.
我们知道,[a,b]上的连续函数 f(x)必有最大值与最小值.若又有 f(x)在(a, b)上可导的条件,则由极值点处f ’(x)=0可知最大(小)值点 x0∈{x| f ’(x0)=0或x=a或x=b}.但由于f(x)在[a,b]上连续并不能保证其在(a,b)内可导,而最大(小)值可能出现在f ’(x)不存在的点处(如f(x)=|x(x-1)|,易见最小值为0,出现在点x=0或x=1处,而此时f ’(x)不存在),所以若仅有f(x)在[a,b]连续的条件,为求f(x)的最大(小)值,还需要求出使f ’(x)不存在的点,将这些点处的函数值与诸极值及f(a)、f(b)比较,从而确定最大值与最小值.
根据上述分析,若f(x)在[a,b]上连续,在(a,b)内可导,如果我们可从另外的途径,比如问题的实际背景判断出f(x)的最小值不可能出现在点x=a、x=b处,那么当方程f ’(x)=0在(a,b)内仅有一解x0时,则可断定f(x0)为最小值.
3.求最大(小)值的方法:函数f(x)在闭区间[a,b]上最值求法:
① 求出f(x)在(a,b)内的极值;
② 将函数f(x)的极值与f(a),f(b)比较,其中较大的一个是最大值,较小的一个是最小值.
2.存在性:在闭区间[a,b]上连续函数f(x)在[a,b]上必有最大值与最小值.
1.定义:最值是一个整体性概念,是指函数在给定区向(或定义域)内所有函数值中最大的值或最小的值,最大数值叫最大值,最小的值叫最小值,通常最大值记为M,最小值记为m.
3.判断法则:
① 对于在x0处连续的函数,如果在x0附近的左侧f ’(x)>0,右侧f ’(x)<0,那么f(x0)是极大值;
② 如果在x0附近的左侧f ’(x)<0,右侧f ’(x)>0,那么f(x0)是极小值.
(6)函数的最大值与最小值
2.如果对x0附近的所有点x,都有f(x)>f(x0)称f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),极大值与极小值统称为极值。
1.设函数y=f(x)在x0附近有定义,如果对x0附近的所有点x都有f(x)<f(x0),则称f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0);
4.复合函数的导数
法则:设函数u=g(x)在点x处有导数u’x=g’(x),函数f(u)在点x处的u处有导数y’u=f ’(u);则复合函数y=f[(x)]在点x处也有导数,且 y’x=y’u·u’x,也可简述为:复合函数对自变量的导数,等于已知函数对中间变量的导数乘以中间变量对自变量的导数。
(4)函数的单调性
设函数y=f(x)在某个区间内可导,如果f ’( x)>0时,则函数y=f( x)为增函数;如果f ’(x)<0时,则函数y=f(x)为减函数;如果恒有f ’( x)=0,则y=f(x)为常函数.
(5)函数的极值
3.函数的商的导。
法则:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方.即(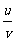 )’=
)’= (v≠0)。
(v≠0)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com